|
|
考研数学中的数列极限存在性证明、中值定理证明题和积分不等式证明题是最难的三个硬骨头,有鉴于此,我对于数列极限证明题给出四类解法、对于积分不等式给出九点开图法,中值定理证明题给出图表法(原谅我起名字这么中二,其实叫什么无所谓)。
对于中值定理类型的题目,无论是辅导书还是视频解析课,都会总结很多类型,而忽略探寻求解中值定理题型思路的一种合理性和顺畅性的方法,即为何不给出一种能够让人思考并像求解函数极限一样的可以牢牢把握住的普适性的解题思路呢?但这一节,我们将只用一种方法解决所遇到的所有中值定理证明题!!!——
即一个图表打遍考研中值定理的所有题型。
图表法包括一个属于自己的图表和标准的三个步骤:
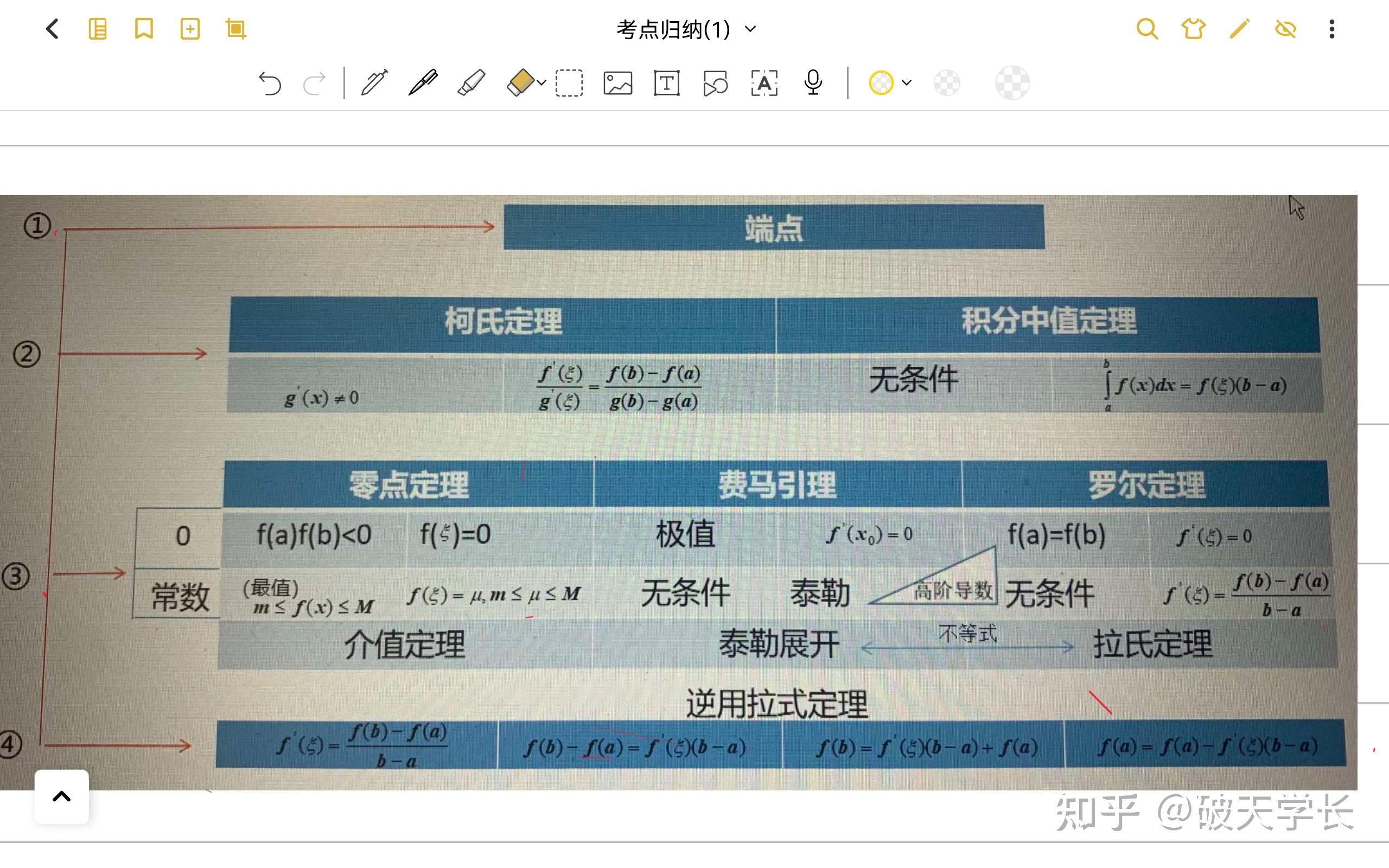
图表
1.排列端点:端点信息要求足够全面,能够把题目中给的所有点按照大小顺序进行排列,并写明每个点的函数值或导数值等。
2.化简结论:将欲证明的结论化简为证等式为0、等式为常数和不等式三种情况(这是选择准确定理的重要依据),并根据是否有原函数确定几阶导,以及将原函数相关信息归到端点处;;
3.查找图表:根据所给信息最多的点和化简后的结论,查找图表,根据图表的条件,确定相关定理。
<hr/>我们通过以下几道例题进行分析。
1.设函数 f(x),g(x) 在 \left| a,b \right| 上连续,在 \left( a,b \right) 内二阶可导且存在相等的最大值,又 f(a)=g(a),f(b)=g(b). 证明:(1)存在 \eta\in\left( a,b \right) ,使得 f(\eta)=g(\eta); (2)存在 \xi\in\left( a,b \right), 使得 f^{&#39;&#39;}(\xi)=g^{&#39;&#39;}(\xi) .
分析:
第(1)问(参照图1):
1.排列端点:题目中除了 a、b 两点外,还包括分别使 f(x_{1})=M,g(x_{2})=M ,易知分为 x_{1}>x_{2} 、 x_{1}<x_{2} 和 x_{1}=x_{2} 三种情况;
2.化简结论:由欲证结论显然可得,待求结论是让证明存在一点使得函数等于0(第一类),并将函数F的信息补充于端点中;
3.查找图表:根据端点 F(x_{1})>0,F(x_{2})<0(其他两种情况类似) ,和结论证存在一点使得函数等数0(第一类),查表可知,符合零点定理的使用条件,结果易得。
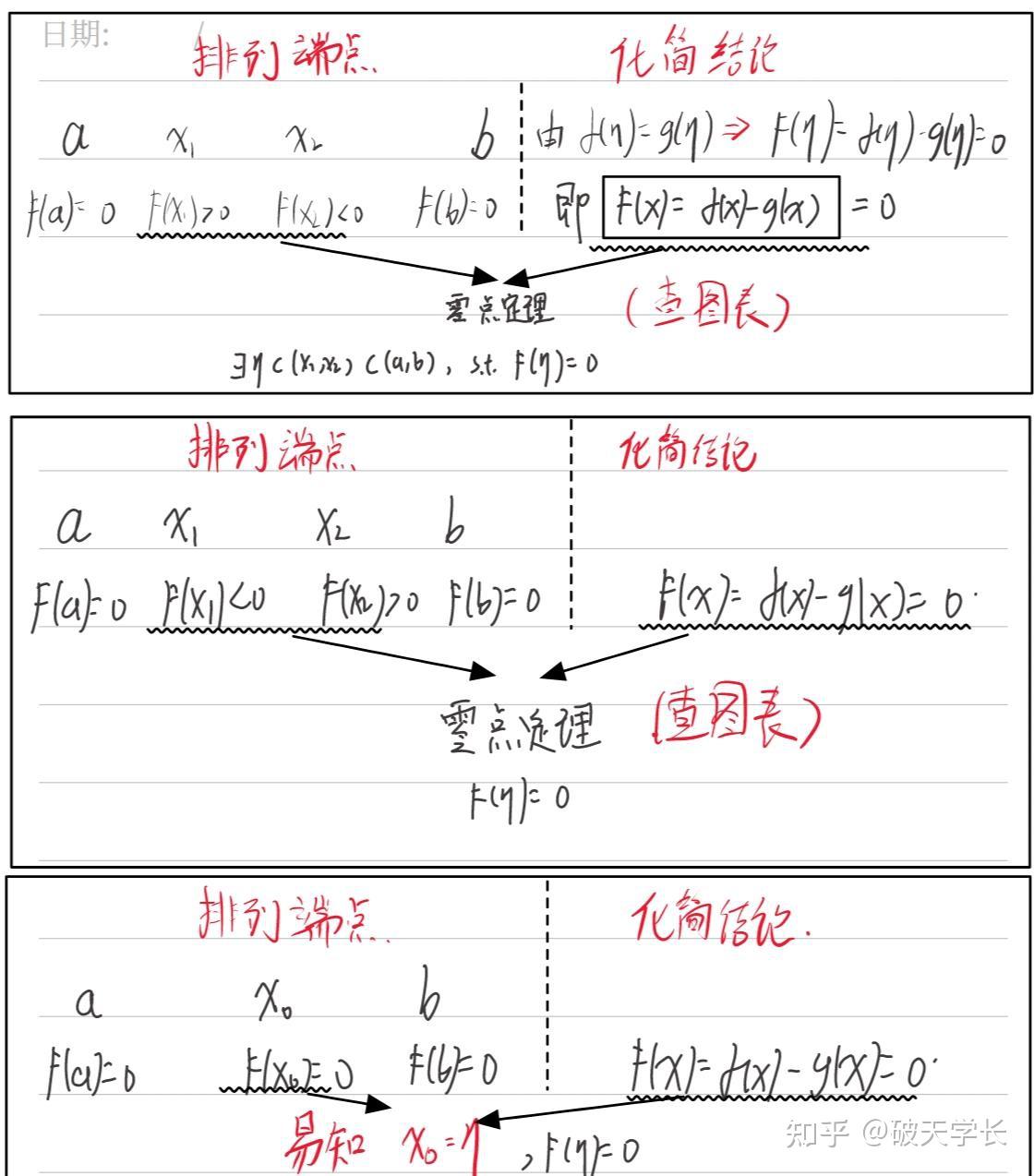
图1
第(2)问(参照图2):
1.排列端点: a、\eta 、 b ;
2.化简结论:由欲证结论显然可得,待求结论是让证明存在一点使得函数等于0(第一类),且为F的二阶导数;
3.查找图表:结论证存在一点使得函数等数0(第一类),且为二阶(高阶),查表可知,仅有罗尔定理符合条件。

图2
<hr/>2.设函数 f(x) 在闭区间 \left[ 0,2 \right] 上具有三阶导数, f(0)=0,f(2)=2 ,且 \lim_{x \rightarrow 1}{\frac{f(x)-1}{lnx}}=1 ,证明:至少存在一点 \xi\in(0,2) ,使得 f^{&#39;&#39;&#39;}(\xi)=0.
分析(参照图3):
1.排列端点:0、1、2,且f(0)=0, f(1)=1,f(2)=2,f^{&#39;}(1)=1
2.化简结论:由欲证结论显然可得,待求结论是让证明存在一点使得函数等于0(第一类),且为 f 的三阶导数;
3.查找图表:结论证存在一点使得函数等数0(第一类),且为 f 的三阶导数(高阶),查表可知,仅有罗尔定理符合条件;再根据罗尔定理要求存在相等的数值的条件和导数,查表易得拉格朗日中值定理。

图3
<hr/>3.设在 (-\infty,+\infty) 上 f^{&#39;&#39;}(x)>0 ,而 f(0)<0 .证明: \frac{f(x)}{x} 分别在 (-\infty,0) 与 (0,+\infty) 上单调增加。
分析(参照图4):
1.排列端点:0、x ,且f^{&#39;&#39;}(x)>0始是(仅证 (0,+\infty) ,至于 (-\infty,0) 类似)
2.化简结论:由欲证结论显然可得,待求结论是让证明存在一点使得函数大于0(第三类),且为 F 的一阶导数;
3.查找图表:结论为不等式(第三类),且为 F 的一阶导数,查表可知,仅有拉格朗日中值定理符合条件。

图4
<hr/>4.设 f(x) 在 \left[ a,b \right] 上有连续导数,若在 \left( a,b \right] 内有一个数 c ,使得 f^{&#39;}(c)=0 .证:在 (a,b) 内必可以找到一点 \xi ,使得 f^{&#39;}(\xi)=\frac{f(\xi)-f(a)}{b-a}.
分析(参照图5):
1.排列端点:a<c\leq b
2.化简结论:由欲证结论显然可得,待求结论是让证明存在一点使得函数等于0(第一类);
3.查找图表:
(1):结论为等于0(第一类),第一类只有三个定理,查表分别是零点定理、费马引理和罗尔定理,必选择其一;
(2):而根据f^{&#39;}(c)=0,查表有费马引理,费马引理要求是取极值,又由f(x) 在 \left[ a,b \right] 上有连续导数,可知, f(x) 存在最大值和最小值,因此,不妨在闭区间 \left[ a,c \right]上取最大值 f(x_{0})=M, 且 f(x_{0})\ne M ,( f(a)=M=m 的情况,结论显然),将这一点带入 F ,易知 F(x_{0})<0 ,
(3)再根据F(x_{0})<0 ,不等式和结论为0(第一类),查表仅有零点定理符合条件,仅需要再构造一个点使得 F>0 即可。
(4)再根据F>0(不等式),和F中存在一阶导数,查表易得拉格朗日中值定理。
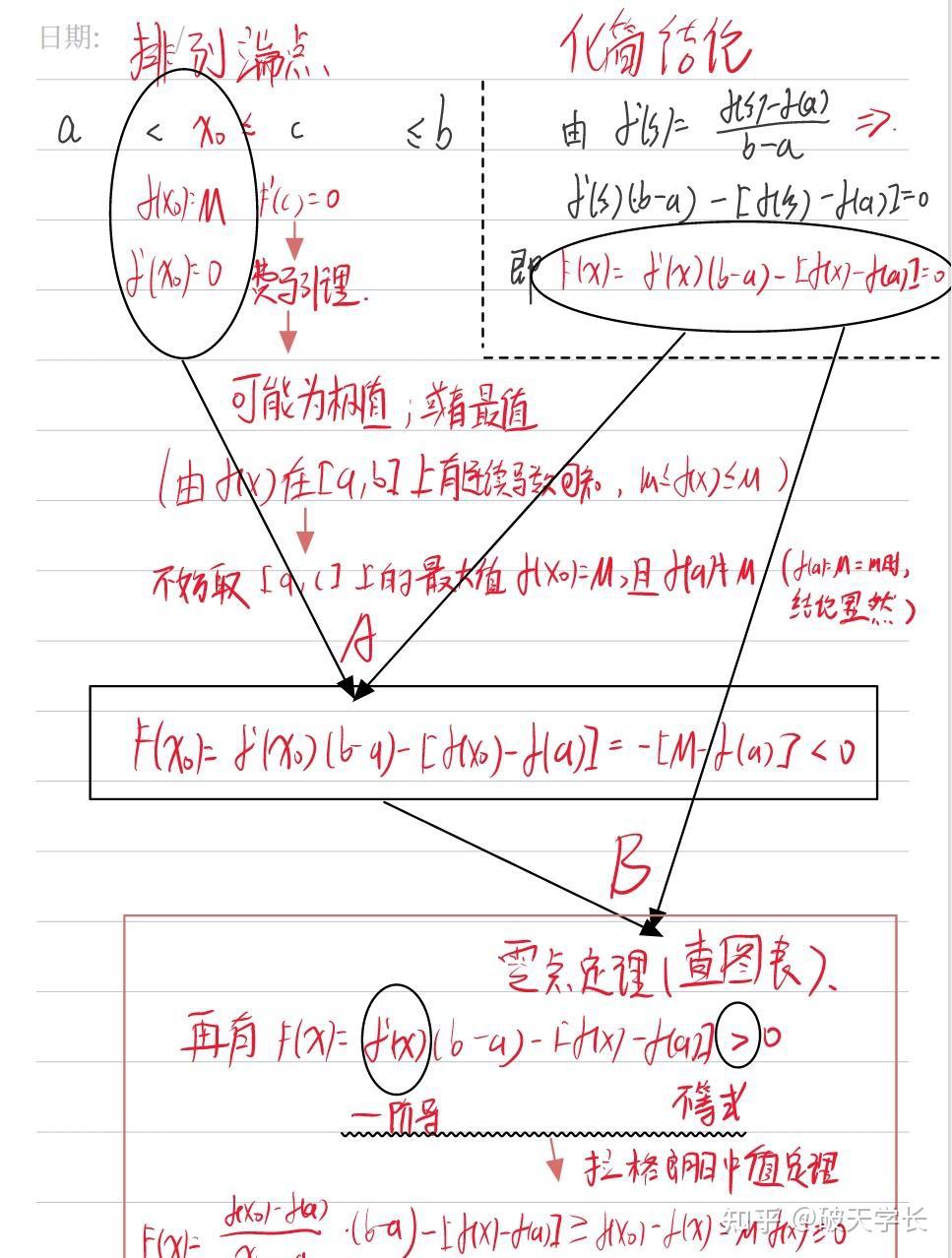
图5
<hr/>5.设函数 f(x) 在 f(x) 在 \left[ a,b \right] 上连续,在 (a,b) 内可导,且 f^{&#39;}(x) 单调增加。证明:在 \left[ a,b \right] 上任意两点 x_{1} 与 x_{2} (x_{1}<x_{2}) ,以及常数 \lambda>0,\mu>0,\lambda+\mu=1, 恒有不等式 f(\lambda x_{1}+\mu x_{2})<\lambda f(x_{1})+\mu f(x_{2}) .
分析(参照图6):
1.排列端点:0、a 、x_{1}、x_{0}=\lambda x_{1}+\mu x_{2}、x_{2}、b
2.化简结论:由欲证结论显然可得,待求结论是让证明不等式(第三类);
3.查找图表:结论为不等式(第三类),且条件有一阶导数,查表可知,仅有拉格朗日中值定理符合条件。

图6
<hr/>6.设函数在闭区间 \left[ -2,2 \right] 上二阶可导,证明:若 \left| f(x) \right|\leq1(x\in\left[ -2,2 \right]), 且 \frac{1}{2}\left[ f^{&#39;}(0) \right]^2+\left[ f(0) \right]^2>\frac{3}{2} ,则比存在 x_{0}\in(-2,2), 使得 f^{&#39;&#39;}(x_{0})+3\left[ f(x_{0}) \right]^2=0.
分析(参照图7):
1.排列端点:-2、0、2
2.化简结论:由欲证结论显然可得,待求结论是让证明等于0(第一类),且为F的一阶导;
3.查找图表:结论为等式(第一类),且条件有一阶导数,查表可知,可选择罗尔定理或费马引理;
又根据 \left| f(x) \right|\leq1 (不等式)和F中存在一阶导数,查表可得拉格朗日中值定理;
再根据闭区间存在最大值和在区间断点处不取最值的条件,查表可得费马引理。

图7
总结:实际上,中值定理图表法的过程通过简单的做几道题即可熟练掌握,但,关键在于图表这个东西,你要非常熟练,他的每一行每一列,每一个字你都要非常清晰,当你查找图表时,只要有两个或两个以上的条件满足于图表中的某个定理时,那么大概率就是这个定理,当你做的题目足够多时,你会对这个图表进行更新变革(所以之歌图表并不是一成不变的,而是随着你的理解而逐渐修正,唯一不变的是图表一定足够简洁),你会发现,中值定理的条件与结论无非是这么一张表格,熟练操之,中值定理不过如此,如有不懂或不清晰的地方,欢迎私聊我一起讨论。
当你使用图表法做考研范围内的中值定理的题目时,如果发现做不出来,请再仔细查看端点信息是否全面、图表是否有疏忽的地方即可。
注意:不知道大家注意到没有,这几道例题并没有涉及积分!!!,如果涉及积分,那就是另一个话题了,如有时间,我会再更新关于积分不等式(或等式)的九点开图法。 |
|