|
|
@(Soft Matter Physics)
晶体指的是在空间排列上展现出一定的规律性的结构。一般所指的固态晶体有很高的空间对成性,原子(或者分子)在空间上有规律性地排列形成周期结构。一般概念里的液态,是在热力学温度高于其分子间相互作用力后所展现出的不定形状态,由于其无法维持稳定结构,其构成也自然没有规律性。而这里所讨论的液晶,则是一种介于固态晶体和液体之间的状态。其宏观上有不定形的特性,但微观排列上却有一定规律。
由于其有不定形的特性,其分子排布的空间有序性被一定程度破坏。而一个分子具有六个自由度,包含三个转动自由度 (\alpha,\beta,\gamma) 以及三个平动自由度 (x,y,z) 。其平动自由在温度上升的过程中不断被打开而破坏空间有序性,那么其有序性主要由转动自由度贡献。而液晶,则正是失去了一定空间有序性(位置序 positional order)而保留了取向的(取向序 orientational order)的一种材料。
既然需要液晶保有取向序,那其构成分子必定是各向异性(anistropic)。各项异性可以是其形态上的各向异性,也可以是作用力层面的。由此液晶又被分为两类,热致液晶(Thermotropic liquid crystal)和溶致液晶(lyotropic liquid crystal)。前者在结构上非球体,可再细分单轴(uniaxial), 双轴(biaxial) 。后者是具有亲水输水性质的分子配成水溶液而实现。
水溶晶体留到后面,接下来关注的是热力学晶体。而为了简化,主要关注单轴液晶。所谓单轴,是指分子有一个轴向,也就是为柱对称结构。考虑到分子在轴向上的尺度,又可以细分为棒状(rod-like)和盘状(disk-like)。
2.1 碟状 Discotic Liquid Crystals
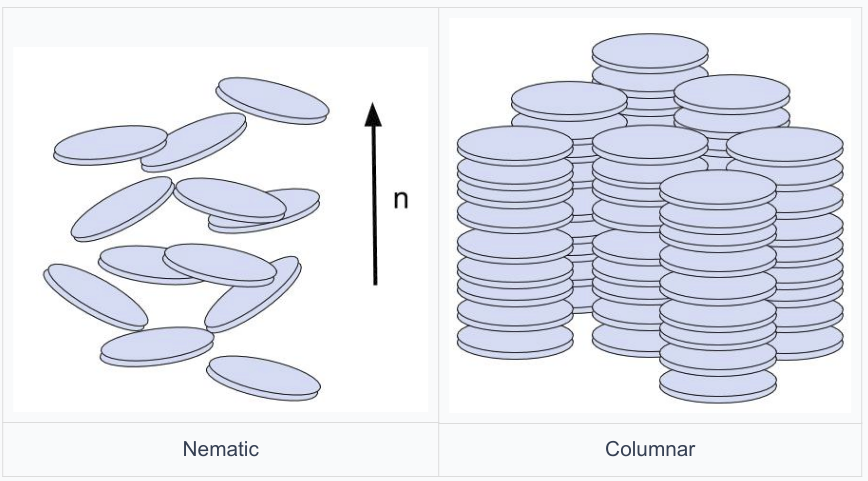
Fig 1. 两类碟状液晶
2.1.1 向列型碟状液晶 Nematic Discotic
向列型碟状晶体与向列型棒状晶体本质上相同,空间的有序性被完全破坏但是方向的有序性被保留了下来。
2.1.2 柱碟状液晶 Columnar Discotic
在柱碟状液晶中,碟状分子先通过层叠形成柱体,而柱体具有一定的排列。在柱体长轴方向的方向有序性是被很自然破坏的,而垂直方向的方向序有一定保留。取向有序性被很好的维持。
2.2 棒状 rod-like

Fig2. 从低温到高温的物态改变[1]
如上图所示,棒状分子在由低温到高温的过程中,经历了如下过程:
- 晶体态(Crystalline Solid):空间分布和方向分布都保有的固态象
- 层列型液晶态(Smectic):一定程度上任然保持层状结构,但是分子在取向上呈现了
- 向列型(Nemtic):失去了位置序,没有层状结构,但是整体取向上仍然有一致性。
- 各项同性(Isotropic):随着温度继续升高,完全失去了有序性的各项同性状态。
备注:在固态晶体到层列型液晶间还有一类软晶体。
2.2.1 层列型液晶 Smectic phases
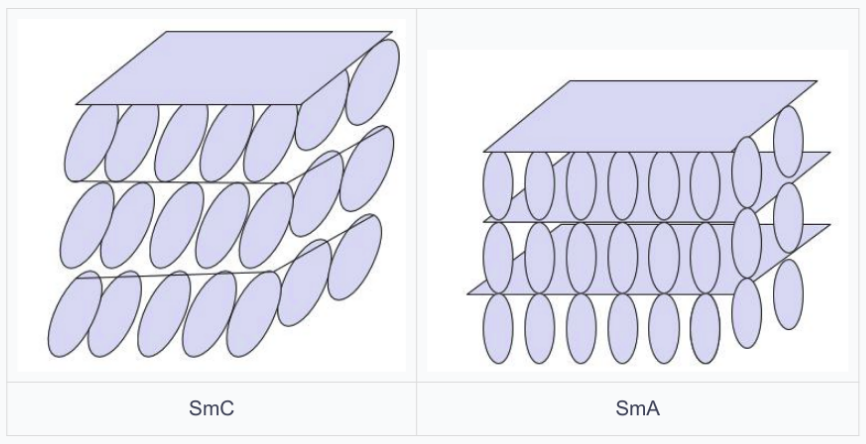
Fig 3. 两类层列型液晶
层列形液晶指的是液晶还保有一定的空间分布规律,形成层状结构,在同一层的分子没有长程空间有序性,可以认为是二维上的液态。从对对成型的破坏来看,二维平面上的两个自由度被打开。而对取向有序性的破坏,还可以细分为更多的中间态。
SmA相,分子是主要垂直于分界面的
SmC相,分子相对于分界面有了顷角
短程位置序结构 (SmB, SmF,SmI)
在层列型液晶的分类中还存在一类拥有短程空间有序性的结构(二维面),称为六角相(Hexatic phase)。在此类液晶中,分子会有六角形的绑定,单这种有序结构只会存在与局部,而无法蔓延到整个晶体。
2.2.2 向列型液晶 Nematic phase
向列型液晶具有以下特征:
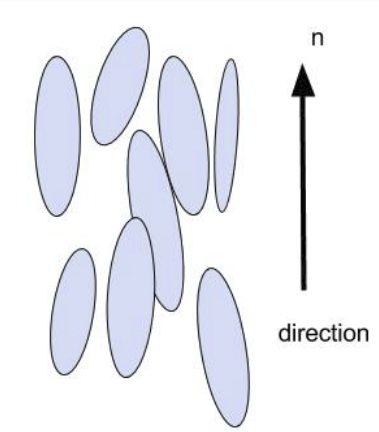
Fig 4. Nematic Phase
1. 拥有取向序
2. 不具有位置序,即空间分布规律性
3. 易于流动
向列型液晶不再具有层列型液晶的层状结构,可见这里空间序被完全破坏了,也就是三个平动自由度被完全打开。但其仍然保持了取向的长程关联性(有序性)。
2.2.3 胆固醇液晶 Cholesteric
胆固醇液晶是由手性分子形成的Nematic phase, 现在又被称为手性向列型 (Chiral Nematic)。由于分子的手性而引起宏观上的手性。
3.描述方法
3.1 指向矢 Director
指向矢(director)是用来表征液晶整体指向的一个方向向量。其根据分子长边的指向平均得到,之前的图中n表示这个指向矢量。该平均是对于局部的一个统计平均,对于一般的Nematic phase,局部的统计平均与全局平均应该是相吻合的,但是对于胆固醇液晶,我们会发现指向矢量会螺旋性地变换方向。
3.2 序参量 Order Parameter
对于任何一个统计系统,序参量当然是最重要的指标物理量。序参量,如其名,用来表征整个系统的有序程度。对于Nematic liquid cyrstal,我们根据取向序定义序参量。一般使用的是二阶序参量
\begin{equation}S_2=\langle \frac{3\cos^2{\theta}-1}{2}\rangle \end{equation}
即是Legendre级数的第二项的平均。我们将在接下来的一篇中详细讨论这个序参量。
3.3 相变 Phase transitions
凝聚态物质在不同状态之间的转变称之为相变。根据郎道相变理论,可以分出
一阶相变,二阶相变以及更高阶的相比那。一阶相变为序参量不连续的相变,二阶相变为序参量连续但是其一阶导数不连续的相变,以此类推。这里由SmA转向SmC的相变为二阶相变,而由SmC转向Nematic phase的相变为一阶相变,细节将在下一篇中讨论。
3.4 相互作用力
液晶的方向有效性是根据什么作用维持的?这是从物理角度描述液晶的关键。我们知道热力学涨落表现是使得系统更加无序,那么我们便需要一个分子间的作用力去抵消热力学涨落的作用,候选的有偶级子(dopole-dipole)作用力,或更弱的范德华力,或直接处理为刚体的方式。究竟那种力才能实现我们液晶的性质将在接下来的文章中进一步讨论。
参考文献
1. Hamley, Ian W. Introduction to soft matter: synthetic and biological self-assembling materials. John Wiley & Sons, 2013.
2. Sengupta, Anupam. Topological microfluidics: nematic liquid crystals and nematic colloids in microfluidic environment. Springer Science & Business Media, 2013. |
|