|
|
A. Everybody Likes Good Arrays!
题意
现有 a 数组,设一次操作如下:
- 选择相邻的两个元素,将两个元素删除,然后添加它们的乘积。
请执行尽量少的操作,使得:
代码
void solve()
{
int n; cin >> n;
int a[n+1];
for(int i=1;i<=n;i++) cin >> a;
for(int i=2;i<=n;i++)
{
if(a%2 == a[i-1]%2) ans++;
}
cout << ans << &#39;\n&#39;;
}
B. Emordnilap
题意
对于 (1,2,\cdots,n) 的每一个排列 p ,设 p&#39; 是翻转这个排列后得到的排列,设 p&#39;&#39; 是 p 与 p&#39;&#39; 拼接的结果,例如 p=(1,3,2)\to p&#39;&#39;=(1,3,2,2,3,1)
设 f(p) 是 p 对应的 p&#39;&#39; 的逆序对数量。求 \sum f(p)
分析
对于一个长度为 2n 的 p&#39;&#39; ,它的逆序对由三部分组成:
- 左半部分 p 内部的逆序对。
- 右半部分 p&#39; 内部的逆序对。
- 左半部分的某个数 u 和右半部分某个数 v 组成的逆序对。
第一部分与第二部分的逆序对数量之和一定是 \frac{n(n-1)}{2} 。设想若在 p 中有 p_i>p_j 且 i<j ,翻转后一定不存在这一对逆序对(因为 p_i 被翻转到 p_j 右侧,是正常顺序);反之亦然。因此对于每一对 (i,j) ,它们只在 p 和 p&#39; 中的一个排列里有 1 个逆序对的贡献。
第三部分的答案是 \frac{n(n-1)}{2} ,考虑左半部分的 1 ,不能产生任何逆序对;左半部分的 2 和右半部分的 1 会产生 1 和逆序对;左半部分的 3 和右半部分的 1,2 各产生一个逆序对。因此逆序对的总数是 0+1+2+\cdots+n-1=\frac{n(n-1)}{2} 。
答案是 n(n-1)n! 。
代码
Mint 是实现的自动取模类,Fac表示阶乘。
void solve()
{
int n; cin >> n;
cout << Mint(n) * (n-1) * Fac(n) << &#39;\n&#39;;
}
C. Quiz Master
题意
在数组 a 中选取若干元素,构成新数组 b ,使得:
- 对于任意的整数 1\le i\le m , b 中存在某个元素是 i 的倍数。
求数组 b 极差的最小值。
分析
我们对 a 排序,从贪心角度来看,如果我们选取的最小值为 a_l ,最大值为 a_r ,就没有理由不把中间的元素全部纳入 b 数组之中,因此我们可以枚举 l ,寻找最小的 r ,使得条件成立。
注意到,我们可以用双指针的策略处理这一问题。具体来说:
- (1)令 l=1,r=0
- (2)如果当前元素不满足要求,则尝试添加 a_{r+1} ,并令 r 增加 1 。
- (3)将答案与 a_r-a_l 取最小值。
- (4)删除 a_l 。
- (5)令 l 增加 1,如果 l>n ,退出并输出答案。
删除和添加元素的步骤,我们用 cnt 数组来维护, cnt_i 表示有当前有 cnt_i 个元素是 i 的倍数。添加元素时,令所有因子 k 的 cnt_k 增加 1 ;删除元素时则是减少 1 。
代码
void solve()
{
int n, m;
cin >> n >> m;
int a[n+1];
for(int i=1;i<=n;i++) cin >> a;
sort(a+1,a+1+n);
int r = 0, num = 1;
vector<int> cnt(m+1, 0);
// 更新cnt的函数, cnt_i 表示有多少元素是 i 的倍数
auto ins = [&](int x){if(x<=1 || x>m) return;cnt[x]++; if(cnt[x] == 1) num++;};
auto del = [&](int x){if(x<=1 || x>m) return;cnt[x]--; if(cnt[x] == 0) num--;};
int ans = 1e9;
if(m == 1)
{
cout << 0 << &#39;\n&#39;;
return;
}
for(int l=1;l<=n;l++)
{
while(num != m)
{
// 指针移动,加入a[r+1]
if(r == n) break;
for(int i=1;i<=sqrt(a[r+1]);i++)
{
if(a[r+1] % i == 0)
{
ins(i);
if(a[r+1] / i != i) ins(a[r+1] / i);
}
}
r++;
}
if(num == m) ans = min(ans, a[r] - a[l]);
for(int i=1;i<=sqrt(a[l]);i++)
{
if(a[l] % i == 0)
{
del(i);
if(a[l] / i != i) del(a[l] / i);
}
}
}
if(ans == 1e9) cout << -1 << &#39;\n&#39;;
else cout << ans << &#39;\n&#39;;
}
D. Score of a Tree
题意
现有一棵根为 1 的树,其中初始点权是 0 或 1 ,共有 2^n 种状态。
每一秒,一个点的点权变为上一秒其所有孩子的点权的异或值。
设:
- S(t) 是第 t 秒,所有结点的点权和。
- f(A) 是初始点权分布为 A (一个长为 n 的 0/1 数组,代表了所有结点的点权)时,在第 [0,10^{100}] 秒范围内的 S(t) 的和。
求 \sum f(A)
分析
针对每一结点,我们可以证明:
- 若第 t 秒,存在一个孩子满足:
- 在一半的情况下表现为 0 (指的是对于一半的初始点权分布而言,在第 t 秒它将表现为 0 ),一半的情况下表现为 1 。
- 则它在第 t+1 秒也满足这一条件。
我们取一个满足条件的孩子,设其他孩子的权值的异或和以 p 的占比能取得 1 ,而 1-p 的占比能取得 0 ,则下一秒当前结点是 0 的占比是 0.5p+0.5(1-p)=0.5 。前半部分是两者均取 1 的情况,后半部分是两者均取 0 的情况。同理 1 的占比也是 0.5 。
我们针对上面提到的“在一半的情况下表现为 0 (指的是对于一半的初始点权分布而言,在这一秒它将表现为 0 ),一半的情况下表现为 1 。”这一性质,设这一性质为 A ,称这样的结点是 A 类结点。
而设“在所有情况下,表现为 0 “是性质 B ,这样的结点称为 B 类结点。
在上面我们证明了存在孩子为 A 的情况下,父亲在下一秒为 A ;而容易发现所有孩子为 B 的情况下,父亲在下一秒为 B 。
所有结点的初始状态是:
可以证明,设某一结点 i 能向下探索的最大深度(当前深度记为 0 )记为 v_i ,则它将在前 v_i 秒保持为 A ,接下来保持为 B 。
从直观上很好理解,可以参见下图。
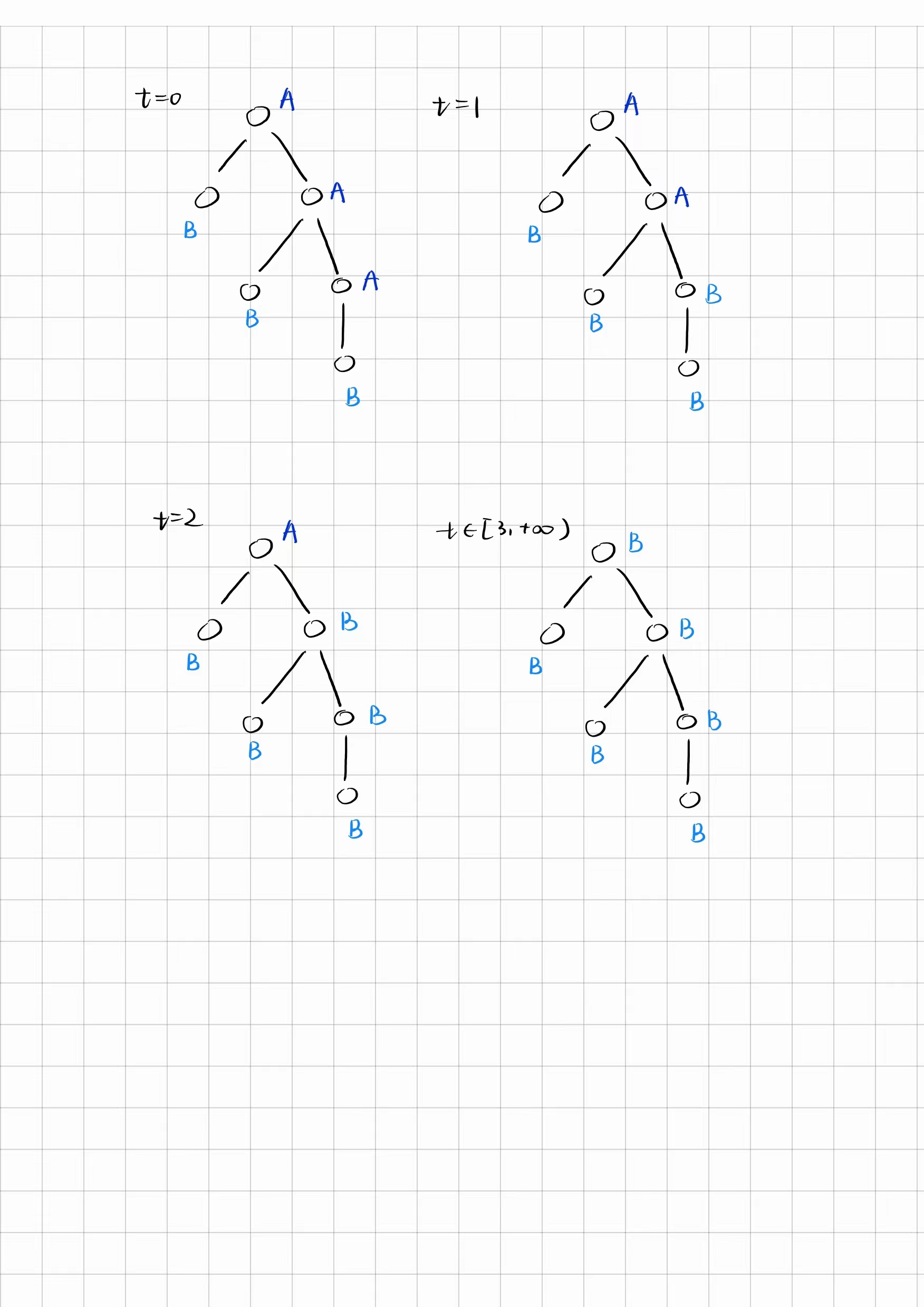
我们采用数学归纳法说明这一点,显然这对于 v_i=0 的所有点成立。若对于所有 v_i=k 的点成立,在 v_i=k+1时:
- 由于它一定存在一个 v_j=k 的孩子,因此它在前 k+1 秒将保持为 A 。
- 由于它不存在任何 v_j>k 的孩子,因此在第 k+1 秒时,所有孩子保持为 B ,因此它在下一秒将转变为 B 。
经过以上漫长的分析,我们可以发现,每个点的贡献其实是 2^{n-1} (表示一半的状态)和 (v_i+1) (表示它在多少秒能保持 A 状态)的乘积,将它们累加即可。
代码
void solve()
{
int n; cin >> n;
vector<int> v[n+1];
for(int i=1;i<n;i++)
{
int x, y; cin >> x >>y;
v[x].push_back(y);
v[y].push_back(x);
}
vector<int> depth(n+1, 0), val(n+1, 0);
function<int(int, int, int)> dfs = [&](int now, int fa, int d){
depth[now] = val[now] = d;
for(auto it : v[now])
{
if(it == fa) continue;
val[now] = max(val[now], dfs(it, now, d+1));
}
return val[now];
};
dfs(1, 1, 0);
Mint ans = 0, tmp = Mint(2).pow(n-1);
for(int i=1;i<=n;i++)
{
ans += tmp * (val - depth + 1);
}
cout << ans << &#39;\n&#39;;
}
E. Edge Reverse
题意
给定有向图,请反转其中任意条边,使得存在一个结点,能到达其他所有结点。
设被反转的边集的权值集合是 \{w_1,w_2,\cdots,w_k\} ,请最小化这一集合的最大值。
分析
假设我们通过反转,可以使得结点 s 能到达任意结点。
此时我们考虑一次反转操作,将 u\to v 的边反转。
- 我们可以决定是否反转这条边,当 s 可以到达 u 的情况下,则一定能到达 v ; s 可以到达 v 的情况下,通过一次反转也可以到达 u 。
- 如果存在只能通过 s\to u\to v\to t_1 的路径才能到达的点 t_1 ,则一定不存在只能通过 s\to v\to u\to t_2 的点 t_2 ,因为从上述条件可看出 s 不经过 u,v 之间的边也可到达 u ,所以直接 s\to u\to t_2 即可。反之亦然,这是为了证明下面&#34;连双向边&#34;的合理性,不存在&#34; s 到达某些点需要正向边,另一些需要反向边,因此连双向边不合法&#34;的情况。
- 因此 u 和 v 可以看成一个整体。在实现中,我们可以看作 u,v 间存在双向边。
我们二分最大权值,对于权值小于二分值 w 的正向边,考虑连一条反向边,接下来的问题就变为:
这是一个经典的问题,我们利用 tarjan 算法将图缩为 DAG,接下来只要判断入度为 0 的点是否为一个即可。因为:
- 入度为 0 的点不可能由其他点到达,如果数量超过 1 个,显然不可行。
- 否则从该点出发,一定能到达其他点,考虑以下 bfs 过程即可:
- 一开始队列中只有当前点 u 。
- 每次将相邻点加入队列后,就从图中删除队首以及它引出的所有边。
- 我们预想剩余的图应当是空图,反设不然,剩余的图必然会存在入度为 0 的点(否则会有环),它也一定不是由于删除某个结点 v 造成的(否则 u 可以到达 v ,再到达该结点),只能是一开始它的入度就为 0 ,这与假设矛盾。
代码
一开始的连通性判断写 dfs 也可以。
tarjan部分抄了 oi-wiki 的代码。
ll lower(ll start, ll end, ll target, function< ll(ll) > func)
{
// if(func(end) < target) return end + 1;
ll l = start, r = end;
while (l < r) {
ll mid = (l + r) / 2;
if (func(mid) < target)
l = mid + 1;
else
r = mid;
}
return l;
}
struct dsu{
vector<int> p;
dsu(int n) {p.resize(n + 1); for(int i = 1; i <= n; i++) p = i;}
int find(int x) {if(x != p[x]) p[x] = find(p[x]); return p[x];}
void merge(int x, int y) {p[find(x)] = find(y);}
};
void solve()
{
int n, m; cin >> n >> m;
vector<array<int, 2>> v[n+1];
dsu d(n);
for(int i=1;i<=m;i++)
{
int x,y,z; cin >> x >> y >> z;
v[x].push_back({y, 0});
v[y].push_back({x, z});
d.merge(x,y);
}
// 并查集判断是否连通
set<int> s;
for(int i=1;i<=n;i++) s.insert(d.find(i));
if(s.size() != 1) {cout << -1 << &#39;\n&#39;; return;}
cout << lower(0, 1e9, 1, [&](int limit){
vector<int> dfn(n+1, 0), low(n+1, 0),
s(n+1, 0), in_stack(n+1, 0);
int tp = 0, dfncnt = 0;
vector<int> scc(n+1, 0);
int sc = 0;
vector<int> sz(n+1, 0);
function<void(int)> tarjan = [&](int u) {
low = dfn = ++dfncnt, s[++tp] = u, in_stack = 1;
for(auto [to, w] : v){
if(w > limit) continue;
if (!dfn[to]) {
tarjan(to);
low = min(low, low[to]);
} else if (in_stack[to]) {
low = min(low, dfn[to]);
}
}
if (dfn == low) {
++sc;
while (s[tp] != u) {
scc[s[tp]] = sc;
sz[sc]++;
in_stack[s[tp]] = 0;
--tp;
}
scc[s[tp]] = sc;
sz[sc]++;
in_stack[s[tp]] = 0;
--tp;
}
};
for (int i=1;i<=n;i++)
if (dfn == 0) tarjan(i);
vector<int> ind(n+1, 0); // 入度个数
for(int i=1;i<=n;i++)
{
for(auto [j, w]: v)
{
if(w > limit) continue;
if(scc != scc[j]) ind[scc[j]]++;
}
}
int zero_cnt = 0;
for(int i=1;i<=sc;i++)
{
zero_cnt += (ind == 0);
}
return zero_cnt == 1;
}) << &#39;\n&#39;;
} |
|