|
|
写点统计力学哦。
首先明确,统计力学的研究对象是微观粒子,但研究目的却是确定系统的宏观性质,比如确定压强、内能、温度等等。统计力学中存在一个基本假设:等概率原理,即处于平衡态的孤立系统,任意微观状态出现的概率相等。也就是说,可以把微观状态看作基本事件,用高中学过的古典概型去研究统计力学哦。
那么首先应该研究哪个宏观性质比较好呢?学过热学的伙伴们可能会觉得,物态方程那么重要,当然应该研究温度和压强啊。不过呢,温度和压强并不好通过微观性质直接确定,因为它们甚至没有特别明确的微观定义——毕竟它们是宏观物体才有的属性,单个粒子可没有温度和压强!
相反地,内能却是比较容易研究的,因为微观粒子也具有能量。那么我们是不是可以认为,内能就是微观粒子各自的能量之和呢?也就是
E=\sum_i E_i
其中E是内能,在统计力学中常用E而不是U。 E_i 表示第i个粒子具有的能量。这样可不可以呢?

你真要这么觉得,倒也不能说你错。但是,这里的 E_i 必须包含这个粒子的动能和势能。动能还好说,势能......我们知道,粒子之间可不是“老死不相往来”的关系,它们是有相互作用的,这种相互作用就是势能的体现,它应该与粒子之间的相对位置有关。这样看来,每个粒子的势能,还会和其它粒子的相对位置有关?如果用T代表动能,V代表势能,那就是说
E=\sum_i (T_i(p_i)+\sum_{j>i}V_{ij}(x_1,x_2,...,x_i))
其中 p 代表动量。每个V都同时是所有粒子坐标的函数,有时候说不定还会是它们动量的函数。天哪,这太可怕了......所以呢,我们先研究比较理想的情况:近独立子系。
所谓近独立,就是说粒子之间的相互作用很弱,可以忽略不计。也就是说,现在可以认为粒子之间是“老死不相往来”的关系了。所有的 E_i 就仅仅包含了动能,这样的世界是不是美好了很多呢?

接下来我们就要考虑,系统究竟有哪些微观状态?显然,系统的微观状态对应的是系统中每个粒子各自的微观状态。当所有粒子的状态确定时,整个系统的微观状态也就确定了。因此我们现在需要研究粒子可能处于的状态。
根据量子力学,粒子在容器内的能量取值是不连续的,只能取一些分立的值,记为 \varepsilon_1,\varepsilon_2,\varepsilon_3,... 那么每个粒子都有可能处于这些能级上,但别忘了,我们研究的是孤立系统(否则不可以使用等概率原理),所以总能量和总粒子数是恒定的。把第 i 个能级上具有的粒子数记为 a_i ,称 a_1,a_2, a_3,... 构成的集合为粒子数的“分布”,简记为 \{a_i\} 。那么就应该有
N=\sum_ia_i,\space E=\sum_i\varepsilon_ia_i
这里要注意,我们之所以按能量来把粒子分类,是因为我们只关心粒子的能量,而不关心粒子的其它性质。粒子也可能存在两种能量相同的状态,但是这可不方便我们使用“等概率原理”了,毕竟对单个粒子来说,这是两种状态而不是一种!所以呢,我们还要研究每个能级究竟对应了多少种状态,这就是能级“简并度”的概念。同一个能级对应了多少种微观状态,就称这个能级具有多少简并度。我们用 g_i 表示第 i 个能级的简并度。
现在我们自然要问:哪种分布 \{a_i\} 出现的概率最大?根据等概率原理,这其实就是在问,哪种分布对应的微观状态数最多?
这就需要分类讨论了。首先,粒子可不可分辨?也就是说,把两种粒子的状态交换一下,算不算一种新的状态呢?量子力学的全同性原理告诉我们,其实所有粒子都是不可分辨的,但某些特殊情况下,全同性也会不起作用,比如波函数没有重叠的时候。此时粒子就是可分辨的。这种情况称为“定域”,通俗地说,就是所有粒子都只在自己家附近走来走去,没有串门的。

现在我们运用一下高中的排列组合来算一下,对于给定的 \{a_i\} ,可分辨的粒子状态数应该是多少呢?
考虑第一个能级有 a_1 个粒子,我们首先要从N个粒子中挑出 a_1个来,共有 C_N^{a_1} 种挑选方式,然后这 a_1 个粒子又可以在 g_1 个状态中任意选择,每个粒子都有 g_1 种可能的状态, a_1 个粒子就共有 g_1^{a_1} 种可能的状态。第二个能级也作类似考虑,最终再把这些全部乘起来,就得到总状态数
\Omega( \{a_i\})=C_N^{a_1}C_{N-a_1}^{a_2}C_{N-a_1-a_2}^{a_3}...g_1^{a_1}.g_2^{a_2}.g_3^{a_3}...=\frac{N!}{\prod\limits_{i}a_i!}\prod\limits_i g_i^{a_i}
好啦,接下来是不可分辨的情况。实际的粒子不仅不可分辨,还被分为两类:费米子和玻色子。费米子满足泡利不相容原理,即任意两个粒子不能处于完全相同的状态,玻色子则没有泡利不相容原理,但仍然是不可分辨的。通俗来说就是,费米子不喜欢客人,只要一个房子住了人,其它人就都不能进这个房子了,除非里面的人出去。

玻色子则接受群居,可以好多人住同一个房子,但是一旦有两个人进了同一个房子,就分不出谁是谁了。另外注意我这里说的“房子”是粒子所处的能级,之前说可分辨粒子的时候,我说的“房子”是粒子在空间上所处的位置,它们是不一样的哦。
现在让我们用排列组合计算一下玻色子的状态数吧。还记得高中对于相同元素的排列组合是怎么处理的吗?把11个不可分辨的球装进5个箱子里,如果每个箱子都不可以为空的话,有几种装法?

只要用隔板,把球分成5份就好了!分成5份,就需要四个隔板,由于箱子不可以为空,每个隔板可以放的位置就是任意两个球中间,但不能重复放同一个位置。这样,11个球中间有10个位置可以放隔板,所以总共有 C_{10}^4 种放法!是不是很简单呢。下图是隔板法的其中一种分法,它对应的是五个箱子分别放1,2,4,1,3个球。

现在我们希望用这种思路计算玻色子的状态数,但问题是,这种方法假定了箱子不可以为空,而玻色子的某个状态是可以没有任何粒子的,也就是说箱子可以为空。这该怎么办呢?有一个巧妙的办法,就是加入与箱子个数相同的虚拟球!
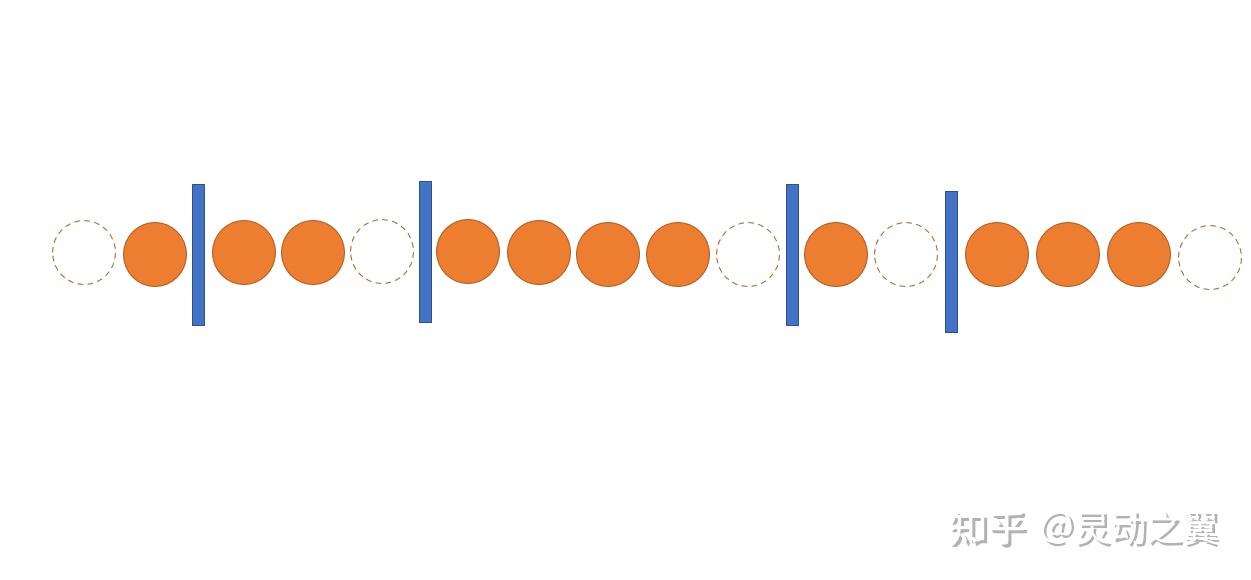
这样,以上题为例,原本11个球就变成了16个球,然后就可以按箱子不可为空的方法去做了。只是当我们得出某个箱子中有3个球时,它其实只有2个球;当某个箱子中有1个球时,它其实没有球,也就是箱子为空了。这种方法就是巧妙地将元素可以为空的问题转化为了元素不可为空的问题。
那么现在我们可以计算玻色子的状态数了。第i个能级具有 a_i 个粒子,它有 g_i 个位置可以占据,利用上面的方法,先假设有 a_i+g_i 个粒子,并插入 g_i-1 个隔板,有 a_i+g_i-1 个位置可以插,所以共有 C_{a_i+g_i-1}^{g_i-1} 种可能的状态。那么所有的粒子具有的总状态数就是
\Omega(\{a_i\})=C_{a_1+g_1-1}^{g_1-1}C_{a_2+g_2-1}^{g_2-1}C_{a_3+g_3-1}^{g_3-1}...=\prod\limits_i\frac{(g_i+a_i-1)!}{a_i!(g_i-1)!}
你可能会发现,在计算可分辨粒子时,我们一开始要先从N个粒子中挑 a_i 个粒子出来,但现在却没有这么做,这是因为粒子不可分辨,怎么挑都是一样的。
好了,最后是费米子。这是最简单的,因为任意位置最多只能有一个粒子,那么对于第i个能级,我们只要在 g_i 种状态中挑选 a_i 种,把粒子放进去就可以了。而且放粒子的时候不需要考虑顺序,因为粒子是不可分辨的。这样就有
\Omega(\{a_i\})=C_{g_1}^{a_1}C_{g_2}^{a_2}C_{g_3}^{a_3}...=\prod\limits_i\frac{g_i!}{a_i!(g_i-a_i)!}
好啦,至此我们推出了三种粒子的状态数。这里再解释一下我们为什么需要“近独立”这个假设,这是因为如果粒子之间有相互作用,粒子的能级就将包含复杂的势能,不同粒子的所有可能的能级不再相同,同一粒子可能的能级也将不再固定,上述方法就完全失效了。
接下来,我们要找出状态数最多的分布。首先是可分辨的粒子,可以看到它的状态数非常复杂,主要表现为阶乘形式。如何处理阶乘呢? \Gamma 函数?多个 \Gamma 函数相乘也是很可怕的......但是,考虑到粒子数 N 通常是很大的,我们可以选择一个很好的近似公式——斯特林公式
n!\sim n^{n}e^{-n}\sqrt{2\pi n}
并且,由于取对数不影响单调性,我们可以把状态数取对数以后再用斯特林公式代换,将会大大简化问题。取对数后的斯特林公式可以近似为
lnn!\approx n(lnn-1)
于是
ln\Omega=N(lnN-1)-\sum_ia_i(lna_i-1)+\sum_ia_ilna_i=NlnN-\sum_ia_iln(\frac{a_i}{g_i})
接下来我们要在满足
N=\sum_ia_i,\space E=\sum_i\varepsilon_ia_i
的约束条件下求解 ln\Omega 的极值,那么我们自然想到要令 ln\Omega 的变分为0。这里要提醒一下,汪志诚、林宗涵和刘川的教材都没有说清楚一个问题,就是在对 ln\Omega 取变分时,他们都得到了
\delta ln\Omega=-\sum_iln(\frac{a_i}{g_i})\delta a_i
然而自己去算过的话,得到的结果应该是
\delta ln\Omega=-\sum_i[ln(\frac{a_i}{g_i}+1)]\delta a_i
这倒不是那三本书都算错了,而是因为上式可以写为
\delta ln\Omega=-\sum_iln(\frac{a_i}{g_i})\delta a_i-\sum_i\delta a_i=-\sum_iln(\frac{a_i}{g_i})\delta a_i-\delta N
而 N 是事先给定的值,故变分为0,因此两式其实是一样的。
要使 ln\Omega 取极值,就要让它的变分为0,也就是令
\sum_iln(\frac{a_i}{g_i})\delta a_i=0
如果每个 \delta a_i 都是任意的,就可以轻易得到各项系数 ln(\frac{a_i}{g_i}) 为0的结论,但可惜,由于两个约束条件 N=\sum_ia_i,\space E=\sum_i\varepsilon_ia_i 的存在,至少有两个 \delta a_i 不是任意的。比如有 n 个 a_i ,那么当 n-2 个 \delta a_i 选定时,剩下的两个 \delta a_i 就可以用这两个约束条件算出来了, 不再可以任意选取。不过呢,由于 \delta N=\delta E=0 ,我们可以把极值条件改写为
\sum_iln(\frac{a_i}{g_i})\delta a_i=\sum_iln(\frac{a_i}{g_i})\delta a_i+\alpha\delta N+\beta\delta E=\sum_i[ln(\frac{a_i}{g_i})+\alpha+\beta\varepsilon_i]\delta a_i=0
其中 \alpha,\beta 为两个常数,称为拉格朗日乘子。现在依然至少有两个 \delta a_i 不是任意的,所以不能得出 ln(\frac{a_i}{g_i})+\alpha+\beta\varepsilon_i=0 的结论,但现在我们有两个未定的拉格朗日乘子 \alpha,\beta 呀!我们可以让 \delta a_3,\delta a_4, \delta a_5,... 都任意变化,这样 \delta a_1 和 \delta a_2 都不能任意选取,但我们总可以选取合适的 \alpha 和 \beta 使 \delta a_1 和 \delta a_2 满足
ln(\frac{a_1}{g_1})+\alpha+\beta\varepsilon_1=0,ln(\frac{a_2}{g_2})+\alpha+\beta\varepsilon_2=0
剩下的 \delta a_i 都可以任意变化,所以必然满足
ln(\frac{a_i}{g_i})+\alpha+\beta\varepsilon_i=0,i\geq3
综合起来, ln(\frac{a_i}{g_i})+\alpha+\beta\varepsilon_i=0 就对任意的 i 都成立了。由这个式子我们可以得到
a_i=g_ie^{-\alpha-\beta\varepsilon_i}
这就是可分辨的粒子满足的能级分布,称为玻尔兹曼分布或麦克斯韦-玻尔兹曼分布。其中 \alpha 和 \beta 要根据两个约束条件来确定。从这个公式可以看出,能量越大的能级,粒子数越少,也就是说大部分粒子倾向于处在低能量的状态,是不是很合理呢?
用同样的方法可以得到费米子和玻色子的分布,不过需要对简并度 g_i 也使用斯特林公式。进行一些近似以后可以得到
a_i=\frac{g_i}{e^{\alpha+\beta\varepsilon_i}\pm1}
其中取正号代表的是费米子的分布,称为费米分布或费米-狄拉克分布;取负号代表玻色子的分布,称为玻色分布或玻色-爱因斯坦分布。这一点不难理解:费米子不允许两个粒子处于同一个状态,那么同一能级的费米子数量自然会更少一些,所以分母自然是加号而不是减号啦。另外可以看到,如果把上式的1改为0,这就变成玻尔兹曼分布了。
但是这个推导好像有点不对啊,斯特林公式只能在 n 很大的时候近似成立吧,那为什么可以对简并度使用斯特林公式?还有 a_i ,它也不一定很大啊?为什么可以用?
所以呢,这个推导其实是有点问题的,正规的方法应该是用系综理论推导出上面的三种分布。
那么这部分内容就是这些啦,下次再见哦! |
|