|
|
·排列
一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列(permutation). 这是课本上的定义.主要是与组合区分开:组合是无序的,排列是有序的.
排列数公式A_{n}^{m}=n(n-1)(n-2)\dots(n-m+1).
A_{n}^{m}=\frac{n!}{(n-m)!}.
我的理解是,从n开始依次乘下去,每次减1,乘m个.
·组合
一般地,从n个不同的元素中,任取m(m≤n)个元素为一组,叫作从n个不同元素中取出m个元素的一个组合(combination). 组合数公式 C_{n}^{m}=\frac{A_{n}^{m}}{A_{m}^{m}}
感觉记着一个就够了.
·题目
我以限制条件分类.
无限制
这种只要区分排列/组合/其他就行了.
例1:北京、上海、香港三个民航站之间的直达航线,需要准备的不同的飞机票的种数为____.
因飞机票计顺序,故用排列A_{3}^{2}=3\times2=6 . 例2:将7名学生分配到甲、乙两个宿舍中,每个宿舍至少安排2名学生,不同的分配方案有多少种?
转化为一个宿舍学生的问题.甲宿舍中学生数为2~7;而宿舍中人员无所谓顺序,由分类加法计数原理,有 C_{7}^{2}+ C_{7}^{3}+ C_{7}^{4}+ C_{7}^{5}=C_{8}^{3}+ C_{8}^{5}=2C_{8}^{3}=112. 尤其体现在送书问题上:
例3:(1)6本不同的书全部送给5人,有多少种不同的送书方法?
尽管是不同元素,但没有”取出“的意思,既非排列亦非组合,由分步乘法计数原理,有 5^6 种. (2)5本不同的书全部送给6人,每人至多1本,有多少种不同的送书方法?
不同的书且每人至多1本,为排列问题,有 A_{6}^{5}=6\times5\times4\times3\times2=720 种. (3)5本相同的书全部送给6人,每人至多1本,有多少种不同的送书方法?
既然相同的书,便无所谓顺序,为组合问题,有 C_{6}^{5}=C_6^1=6 种. 有限制
有限制就很麻烦,且分多种情况,只能在做题中积累了.基本方法有特殊位置、特殊元素优先处理,间接法,捆绑法,插空法,缩倍法,隔板法.
① 相邻
一般用捆绑法和插空法来处理.
所谓捆绑法,就是将相邻元素捆为一个,作一个元素处理.此时应注意其内部排列.
所谓插空法,就是用不相邻元素插其他元素的空.此时应注意其他元素排列.
例4:有5盆各不相同的菊花,其中黄菊花2盆、白菊花2盆、红菊花1盆,现把它们摆放成一排,要求2盆黄菊花必须相邻,2盆白菊花不能相邻,则这5盆花不同的摆放种数是____.
黄菊花必须相邻,用捆绑处理,将2盆黄菊花捆为一个元素.因5盆菊花各不相同,应考虑其内部排列 A_{2}^{2} ;白菊花不相邻,用插空处理.现将其他元素(2盆黄菊花、红菊花)全排列 A_{2}^{2} ,有3个空;用白菊花插空,顾及顺序,有 A_{3}^{2} .由分步乘法计数原理, 有A_{2}^{2}\cdot A_{2}^{2}\cdot A_{3}^{2}=2\times2\times3\times2=24 种. 例5:6把椅子排成一排,3人随机就坐,则:
(1)任何两人都不相邻的坐法种数有____.
不相邻,用插空法.但此处椅子无所谓顺序,只需插空 A_4^3=24 种. (2)恰有两个空座位相邻的坐法总数有____.
“相邻”则想到捆绑.3个空位是完全相同的,故两个空座位无所谓哪两个;3人有区分,顺序排列 A_3^3 ;将2个不同元素(两个空位、一个空位)插入形成的4个空,有 A_4^2 ;由分步乘法计数原理,有 A_3^3\cdot A_4^2=72 种. ②定序
一般用缩倍法来处理.
有m个不同元素排成一列,其中n个元素之间的先后顺序确定不变,先将这m个元素全排列,有 A_{m}^{m} 种不同的排法;然后任取一个排列,固定其他m-n个元素的位置不动,把这n个元素交换顺序,有 A_n^n 种排法,其中只有一个排列符合题意,因此共有 \frac{A_m^m}{A_n^n} 种满足条件的不同排法.若n个元素定序有多种,应在后面乘上.
例6:将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有几种?
A,B均在C的同侧,则有ABC,CBA,BAC,CAB四种排法.由缩倍法,有 \frac{A_6^6}{A_3^3}\times4=\frac{6!}{3!}\times4=6\times5\times4\times4=480 种. ③ 分配
此类特点是要求每处至少分得数目,并进行分配.
一般用隔板法处理.
例7:将组成篮球队的10个名额分到7所学校,每所学校至少有一个名额,名额分配有多少种?
名额无所谓顺序,只需将学校排成一排,用6个板插入10个名额中的9个空,将其分成7份.有 C_9^6 种. 例8:把20个相同的小球放入编号为1,2,3,4的四个盒子里,要求每个盒子里球的数目不小于盒子的编号数,则一共有______种不同的放法.
先将编号为1,2,3,4的四个盒子分别放入0,1,2,3个球,再把剩下的14个球用隔板法分成四组,有13个空,用3个隔板,故 C_{13}^3 . ④至少/至多/不都是
间接法OR分类处理.
如果反面分类少,就用间接法. C_n^m=C_n^{m-n} 即如此.
例9:如图,某电子器件是由三个电阻组成的回路,其中有6个焊接点A,B,C,D,E,F,如果某个焊接点脱落,整个电路就会不通,现发现电路不通了,那么焊接点脱落的可能性的种数为____.
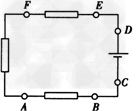
例9
电路不通,即”不都是“焊上的,反面分类少,故间接法 2^6-1=63 种.
若直接法,分类有1)1个没有焊上 C_6^1 ;
2)2个没有焊上 C_6^2 ;
3)3个没有焊上 C_6^3 ;
4)一个没有焊上 C_6^4 ;
5)5个没有焊上 C_6^5 ;
由分类加法计数原理, C_6^1+C_6^2+C_6^3+C_6^4+C_6^5=63 种. 例10:某次运动会,要从4名男志愿者和3名女志愿者中选出3人,分别从事三项不同的工作,若这3人中至少有1名女志愿者,则不同的选派方案的种数有____.
"至少",且反面种数少,可用间接法,用总数 A_7^3 减去无女志愿者 A_4^3 ,得 A_7^3-A_4^3=186 种. ⑤指定
分开处理就好.
例11:甲、乙两人从6门课程中各选修3门,则甲、乙所选的课程中恰有1门相同的选法有____种.
先确定相同的一门 C_6^1 ,再从剩下5门选出甲的 C_5^2 ,再从剩下3门选出乙的 C_3^2 .由分步乘法计数原理,有 C_6^1\cdot C_5^2\cdot C_3^2=180 种. ·闲话
复杂的题多是许多条件的综合,或者是繁杂的分类.实在想不出,也可以列举找思路.尤其要保证自己的式子不重不漏.因为只是预习,并没有做太多题,若见到其他题型,会补充的。 |
|