|
|
根据 3.0节 的讨论,抽象出如下一些概念,进而给出行列式的定义。
一、排列
定义3.1.1 排列、标准排列、逆序
根据 3.0节 的讨论,由于 \text{det}(a_1,a_2,\cdots,a_n) 中任意两个向量的位置发生变化后要变号,因此其符号与向量的排序有关,因此在此提出排列的概念。
排列:把从1到n的n个自然数 i_1,i_2,\cdots,i_n 按任意顺序排成一行 。例如将1到5排列成 (2,1,4,3,5) 。
标准排列:从小到大排列。 (i_1<i_2<\cdots<i_n)
逆序:如果排列中有两个数 i_p,i_q , i_p>i_q,这个组合 ( i_p,i_q) 算一个逆序。
例如:
(1,3,2) 中有1个逆序, (3,2) ;
(3,1,2) 中有2个逆序,分别是 (3,1) 、 (3,2) ;
(3,2,1) 中有3个逆序,分别是 (3,2)、(3,1)、(2,1) 。
一个排序中有几个逆序,其实就是计算机算法中的“冒泡法”恢复标准排列的步骤数。
例如:排列 (4,2,3,1) 中有 (4,2) (4,3) (4,1) (2,1) (3,1) 共5个逆序,而通过“冒泡法”恢复标准排列的步骤数也是5步。 定义3.1.2 逆序数、奇排列、偶排列
逆序数( \tau ):一个排列中的逆序的个数。记作 \tau(i_1,i_2,\cdots,i_n) 。
要数一个排列中的逆序数只用从左到右,数每一个数字右边比其小的数字的个数,然后汇总即可。
反过来,从右向左数每一个数字左边比其小的数字的个数也是一样的。
例如:
\tau(635412)=5+2+3+2+0=12 。即:
6的右边比6小的数字有5个,
3的右边比3小的数字有2个,
5的右边比5小的数字有3个,
4的右边比4小的数字有2个,
1的右边比1小的数字有0个。 奇排列:逆序数 \tau 为奇数的排列。
偶排列:逆序数 \tau 为偶数的排列。
定义3.1.3 对换
将一个排列中的两个数对调位置,其他数的位置不变,称为一次对换。
定理3.1.1 对换对奇偶性的改变
任意一个排列每经过1次对换,其奇偶性发生1次改变。
说明:
(1) 相邻两个数对换,逆序的个数显然要增加1个或减少1个,排列的奇偶性发生1次改变。例如: (6,3,5,4,1,2) 中3、5交换位置,那么逆序增加一个 (5,3) ;
(2) 不相邻的两个数对换转化为多次相邻对换。假设这两个数分别为 i_p,i_q ,并且设它们之间相隔k个数,那么可以让 i_p 和右边相邻的数依次对换位置,直到与 i_q 相邻,这个过程中共发生了k次对换。然后再让 i_q 和左边相邻的数依次对换位置,直到进入 i_p 原来的位置,这个过程中将发生 k+1 次对换。整过过程共计 2k+1 次相邻对换,排列的奇偶性必然发生改变。

示例
定理3.1.2 对换次数的奇偶性
(1) 任意一个排列都可以经过有限次对换变成标准排列。
(2) 一个排列变成标准排列经历的对换次数 s 可能不唯一,但 s 的奇偶性是相同的,并且与排列的奇偶性相同。
说明:
(1) 数学归纳法。
n=1时,显然。
假设已经验证命题对于已知的n元排列成立。
那么,对于n+1元排列 (i_1,i_2,\cdots,i_n,i_{n+1}) ,如果 i_{n+1}\not=n+1 ,那么前面必有一个元 i_k=n+1 。将它们俩对换后就能得到新的排列 (i_1,i_2,\cdots,i_n,n+1) ,而新排列的前n元是可以通过有限次对换到标准排列的。总的次数依然是有限次。
(2) 不唯一:要将排列 (4,2,3,1) 变为标准排列,将 4 和 1 对换, s=1 ,也可以依次将4、2,4、3,4、1对换,得到 (2,3,1,4) ,在此基础上再将1、3,1、2依次兑换, s=3+2=5 。奇偶性:(1) 标准排列的逆序数为0,是偶排列;(2) 定理3.1.1:每一次对换都会改变排列的奇偶性。所以,如果一个排列是偶排列,那么它变成标准排列必须经过偶数次对换;反之,如果它是奇排列,那么它变成标准排列必须经过奇数次对换。 因此有:
(1) (-1)^\tau=(-1)^s 。
(2) \det(e_{i_1},e_{i_2},\cdots,e_{i_n})=(-1)^{\tau(i_1,i_2,\cdots,i_n)} 。 二、行列式的定义
结合上一节和本节讨论,定义,一个 n 阶方阵按照如下方式列出的计算式子称为 n 阶方阵的行列式,简称 n 阶行列式。
记作 \det \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}\\ \end{bmatrix} ,常记作 \begin{vmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}\\ \end{vmatrix} ,也记作 \Delta
\begin{align} =&\sum_{1\leq j_1,j_2,\cdots,j_n\leq n} a_{1j_1}a_{2j_2}\cdots a_{nj_n}\det(e_{j_1},e_{j_2},\cdots,e_{j_n})\\\\ =&\sum_{(j_1,j_2,\cdots,j_n)} a_{1j_1}a_{2j_2}\cdots a_{nj_n}(-1)^{\tau(j_1,j_2,\cdots,j_n)}\\\\ \end{align}
上述结果是根据行向量得到的。
如果按3.0节的列向量得到的结果应该
\begin{align} =&\sum_{1\leq i_1,i_2,\cdots,i_n\leq n} a_{i_11}a_{i_22}\cdots a_{i_nn}\det(e_{i_1}^T,e_{i_2}^T,\cdots,e_{i_n}^T)\\\\ =&\sum_{(i_1,i_2,\cdots,i_n)} a_{i_11}a_{i_22}\cdots a_{i_nn}(-1)^{\tau(i_1,i_2,\cdots,i_n)}\\\\ \end{align}
不过,后面 将说明,这两个结果是相等的。
行列式的本质
就是在每一行(或每一列)抽出一个和其他不同行不同列的系数相乘,根据它们的排列顺序决定在其前面加正号还是负号。
<hr/>三、典例
例1 对角

解:
\begin{align} 原式=&\ a_{14}a_{23}a_{32}a_{41}(-1)^{\tau(4,3,2,1)}\\\\ =&\ a_{14}a_{23}a_{32}a_{41}(-1)^{3+2+1}\\\\ =&\ a_{14}a_{23}a_{32}a_{41}\\\\ \end{align}\\ 例2 上三角、下三角
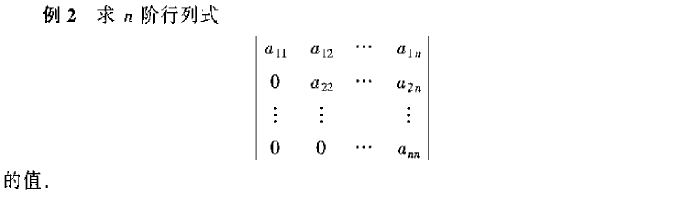
解:因为要在每一行每一列都要抽出一个与其他行不同行不同列的数,所以第1行如果抽了第1列以外的数,那么其它行就一定会抽到第1列的数,从而导致乘积为零。
所以第1行只有抽选第1列的数才有可能使其和接下来选出的其他数的乘积不为零。
而接下来只能在剩下的 (n-1) 行 (n-1) 列中选数,而且又只有选排头的数才可能使选出的数的乘积不为零。
综上所述,选出的乘积不为零的数只有在方阵的对角线上的数。
所以,\begin{align} 原式=&\ a_{11}a_{22}\cdots a_{nn} \end{align} 。 更容易看出,下三角方阵的行列式也是对角线上的数的乘积。
例3 降阶

证明(还不如叫“说明”):
(1)因为右上角的那些分量都是 0 ,所以前 r 行只有前 r 列有必要选,那么后 (n-r) 行就只有余下的 (n-r) 列有必要选了。
结果就是,前 r 行 r 列可以得到 r! 个得数,再乘以后面可以选出的 (n-r)! 个得数,正好就是原式等号后边的形式。
(2)另外,有可能担心的是排列的正负号问题。
因为 j_1,j_2,\cdots,j_r\in\{1,2,\cdots,r\} , j_{r+1},j_{r+2},\cdots,j_{n-r}\in\{r+1,r+2,\cdots,n\},
所以 {\tau(j_1,j_2,\cdots,j_r,i_{r+1},j_{r+2},\cdots,j_{n})} ={\tau(j_1,j_2,\cdots,j_r)}+{\tau(j_{r+1},j_{r+2},\cdots,j_{n})} ,
所以 (-1)^{\tau(j_1,j_2,\cdots,j_r,j_{r+1},j_{r+2},\cdots,j_{n-r})} =(-1)^{\tau(j_1,j_2,\cdots,j_r)}(-1)^{\tau(j_{r+1},j_{r+2},\cdots,j_{n})} 。
综合(1)(2)两点得:
\sum_{j_1,j_2,\cdots,j_n}a_{1j_1}a_{2j_2}\cdots a_{nj_n}(-1)^{\tau(j_1,j_2,\cdots,j_r,j_{r+1},j_{r+2},\cdots,j_{n})}\\
=\sum_{j_1,j_2,\cdots,j_r}a_{j_11}a_{1j_1}a_{2j_2}\cdots a_{rj_r}(-1)^{\tau(j_1,j_2,\cdots,j_r)}\cdot\\\sum_{j_{r+1},j_{r+2},\cdots,j_n}a_{r+1,j_{r+1}}a_{r+2,j_{r+2}}\cdots a_{nj_n}(-1)^{\tau(j_{r+1},j_{r+2},\cdots,j_{n})}\\
=\sum_{j_1,j_2,\cdots,j_r}a_{j_11}a_{j_22}\cdots a_{j_rr}(-1)^{\tau(j_1,j_2,\cdots,j_r)}\cdot\\\sum_{j_{r+1},j_{r+2},\cdots,j_n}a_{j_{r+1}r+1}a_{j_{r+2}r+2}\cdots a_{j_nn}(-1)^{\tau(j_{r+1},j_{r+2},\cdots,j_{n})}\\证毕。

教材上的记法
例3是非常经典的,其实上面的对角、三角、以及下一节要讲到的展开都是这个例的衍生。
<hr/>

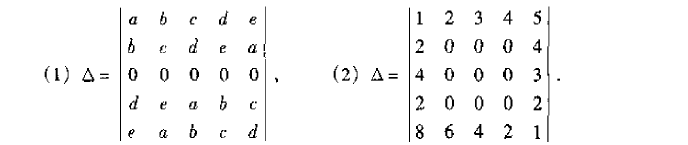
解:(1)挑选到第3行时总是0,所以最终结果是0;
(2)第1行选定后,第2行至多只有2种非0选择,第3行余下1种非0选择,等到第4行就没有非0选项了,所以无论如何,每一种组合到第4行乘积一定为零。因此最终结果为零。 |
|