|
|
摘要: 组合数学的基本模型,以及排列组合的相关公式
【对算法,数学,计算机感兴趣的同学,欢迎关注我哈,阅读更多原创文章】
我的网站:潮汐朝夕的生活实验室
我的公众号:算法题刷刷
我的知乎:潮汐朝夕
我的github:FennelDumplings
我的leetcode:FennelDumplings
<hr/>组合数学的核心内容是深入离散对象的计数方法,而计算机的核心内容是使用算法处理离散数据,因此随着计算机的发展,组合数学也成为了很重要的一个知识点,在力扣上,我们可以找到小几十道相关的题目。以前也拆解过组合数学相关的编程难题:【组合数学】马拦过河卒。
组合数学知识还是有一定的连贯性的,因此想先分几个大部分把组合数学的核心知识点串一遍,然后再慢慢连载一些难题或者趣题。这几个大部分如下:
- 排列组合
- 母函数
- 递推关系
- 特殊计数序列
- 指数型母函数
- 容斥原理
- 鸽巢原理
- 群论
- Polya定理
可以看到内容还是非常的多,但是只要不陷入到证明细节里,就会发现这些都还是属于比较有趣的内容,并且在计算机科学中的应用还是很广泛的。
本文是组合数学系列的第一篇文章,梳理一下组合数学的基本模型,以及排列组合的相关公式,非常基础,建议一定要掌握。主要内容如下:
- 几个例子
- 基本模型:
- 计数原则
- 加法法则,乘法法则
- 放球模型: 排列的递推。分步递推;分类递推
- 格路模型: 杨辉三角,二项式定理
- 排列组合
- 无重排列: 线排列 -> 圆排列 -> 项链排列
- 多重排列: 捆绑法(相邻约束);隔板法(分区域)
- 无重组合
- 可重组合: 构造;不定方程非负整数解;隔板法
- 不相邻组合
- 全排列生成算法: 递归法;字典序法;SJT算法
<hr/>在最开始首先介绍一些组合数学的资料,其中前三本是比较全面的理论性教程,最后一本是不太研究理论而注重应用的。
- 《组合数学》第四版 卢开澄
- 《组合数学》Richard A. Brualdi
- 《组合数学》冯荣权
- 《应用组合数学》[美] 罗伯茨 2007
这几本书也是参考了别人写的博客,书评,以及自己简要翻了翻,自己并没有详细看过,仅供参考,不过后面有时间的话我想楼一眼偏应用的那一本,要是看到什么有趣话题的话就写一写。
<hr/>组合数学发展史
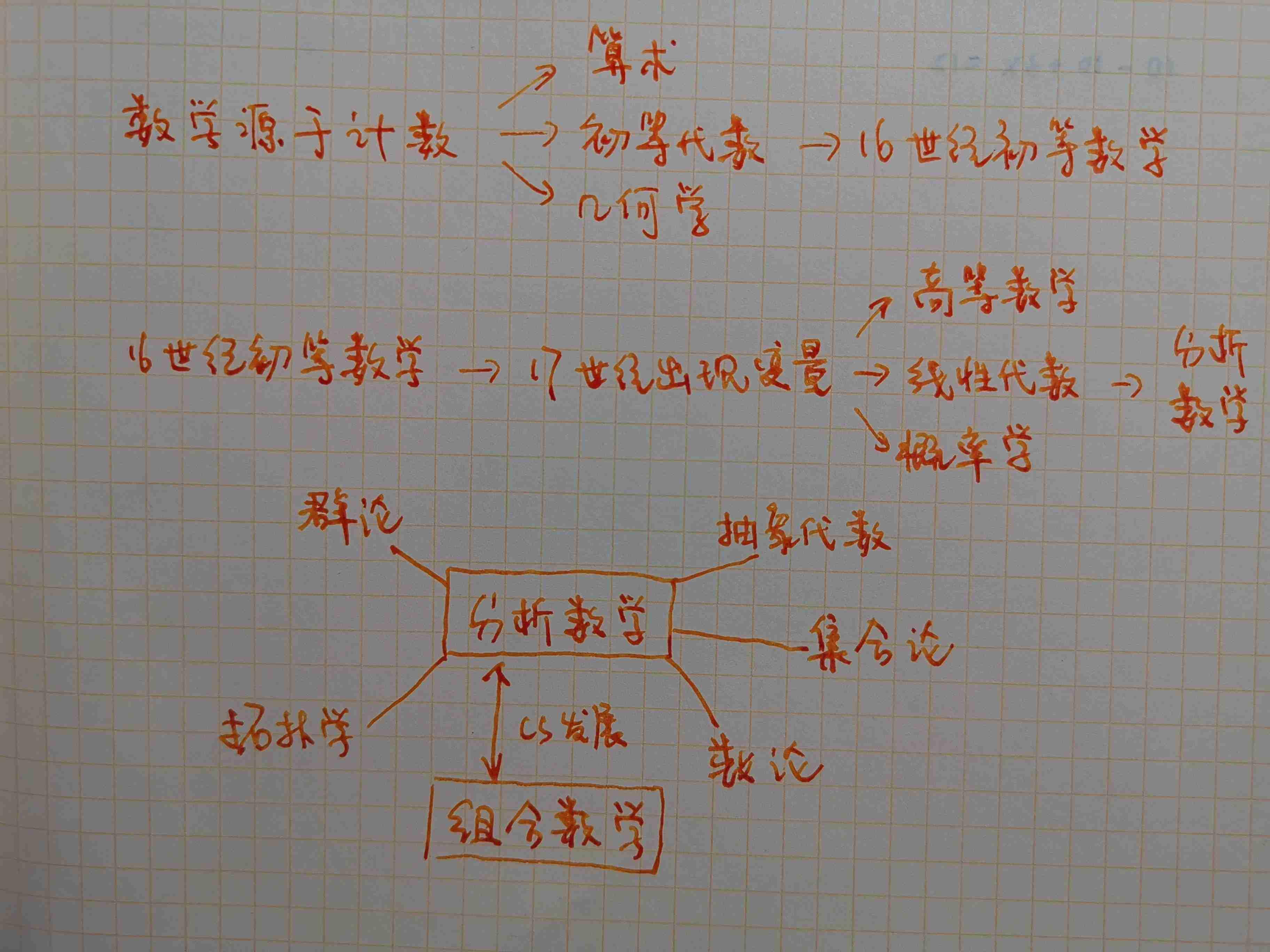
如图,回顾数学的发展历程,有几个关键节点:
首先数学最早起源于计数,由计数引申出三个数学方向:算术、处等代数、几何学。对着发展的深入,到 16 世纪,发展出了初等数学理论体系。
初等数学产生之后,到 17 世纪,出现了变量的概念,进而产生了高等数学、线性代数、概率论,并且随着发展的深入,产生了分析数学的理论体系。
分析数学产生之后,随着计算机的发展,产生了组合数学这一分支。
组合数学是一门研究离散对象的科学。主要研究满足一定条件的离散对象的存在、计数、构造、优化等方面的问题。
组合数学三大问题:
<hr/>一些例子
幻方
阿基米德手稿;14 桥板问题
组合数学名词起源 -- Leibniz, 1666 研究概率时
世界杯淘汰赛有多少场
七桥问题
<hr/>基本模型
计数原则: 无重复,无遗漏
加法法则、乘法法则
(1) 放球模型
- 排列:P(n, r) n 个球取 r 个,放在 r 个不同的盒子
- 组合:C(n, r) (也可以用\binom{n}{r}这个符号) n 个球取 r 个,放在 1 个盒子
P(n, r) = \frac{n!}{(n - r)!} \\ C(n, r) = \frac{P(n, r)}{r!} = \frac{n!}{(n - r)!r!} \\
排列的递推
P(n, r) = nP(n - 1, r - 1) \\
P(n, r) = P(n - 1, r) + rP(n - 1, r - 1) \\
很多组合恒等式可以用放球模型解释
C(n, r) = C(n, n - r) \\ C(n, l)C(l, r) = C(n, r)C(n - r, l - r) \\
(2) 格路模型
杨辉三角
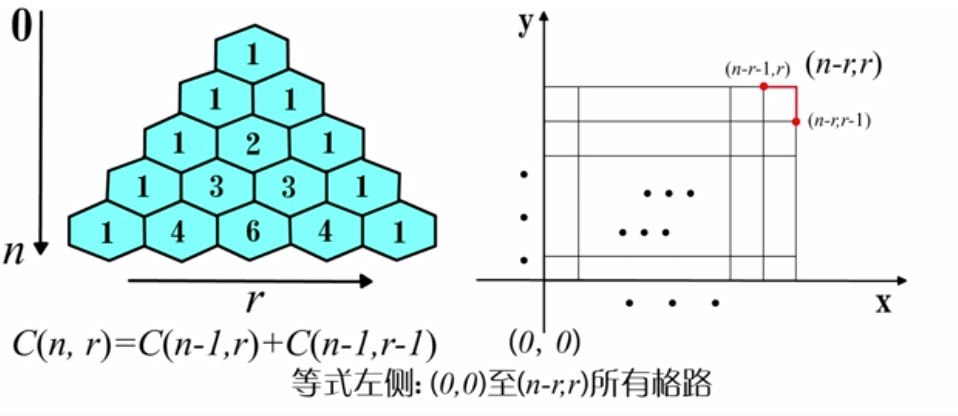
二项式定理
(a + b)^{n} = C(n, 0)a^{n} + C(n, 1)a^{n-1}b + \cdots + C(n, n)b^{n} \\ 2^{n} = C(n, 0) + C(n, 1) + \cdots + C(n, n) \\ 0^{n} = C(n, 0) - C(n, 1) + \cdots \pm C(n, n) \\
格路模型证明组合恒等式
动态规划求组合数的公式:
C(n, r) = C(n - 1, r) - C(n - 1, r - 1) \\
Chu-Vandermonde 恒等式:
\binom{m + n}{r} = \binom{m}{0}\binom{n}{r} + \binom{m}{1}\binom{n}{r - 1} + \cdots + \binom{m}{r}\binom{n}{0} \\
<hr/>排列和组合
线排列 -> 圆排列 -> 项链排列(圆排列基础上再考虑翻转)
- 线排列: P(n, r)
- 圆排列: P(n, r)/r
- 项链排列: P(n, r)/2r
多重排列
P(n; r_{1}, r_{2}, \cdots, r_{t}) = \frac{n!}{(r_{1}!r_{2}!\cdots r_{t}!)} \\(a + b)^{n} = \sum_{0 \lt k \lt n}C(n, k)a^{k}b^{n-k} \\(a_{1}+a_{2}+\cdots+a_{t})^{n} = \sum\frac{n!}{r_{1}!r_{2}!\cdots r_{t}!}a_{1}^{r_{1}}\cdots a_{t}^{r_{t}} \\
隔板法:分区域问题
捆绑法: 相邻约束问题
可重组合
用放球模型,相当于 n 个球有区别,r 个盒子无区别,每盒一个球。
用放球模型,相当于 r 个球无区别,n 个盒子有区别,盒子中球的个数不限。
可重组合计算
(1) 构造相关的无重组合

(2) 不定方程的非负整数解,以下不定方程的非负整数解个数为 C(n + b - 1, b)
x_{1} + \cdots + x_{n} = b \\
(3) 隔板法
不相邻组合
A = \{1, 2, \cdots, n\} 中取 r 个但是相邻元素不能同时取出: C(n - r + 1, r)。
全排列生成算法
(1) 递归法
(2) 字典序法
(3) SJT算法
- 可移动数
- Steinhaus-Johnson-Trotter 算法
|
|