|
|
排列问题:关心顺序,区别对待
三枚奖牌,金银铜颁发给8个人中的3个人,有多少种方法? 换言之:8个人选出3个人进行排名,有多少种方法

第一步:第1名,可以在8个人中任选一个,有8种选择。A可以被替换为 B C D E F G H中的任何一个。
第二步:第2名,可以在除去已经获得金牌的人之外的7个人中任选一个,有7种选择。
第三步:第3名,在已经获得金牌、银牌的两个人之外的6个人中任选一个,有6种选择。
那么很明显,总共的颁奖方式有8 * 7 * 6 种
对8个人都进行排名,有多少种方法?
很明显,从第一名一直到第八名,共有8*7*6*5*4*3*2*1种排法。
发奖牌只发三个就不发了,后面的五个人第几名都不关心了,那么排列问题可以归纳为:

也就是
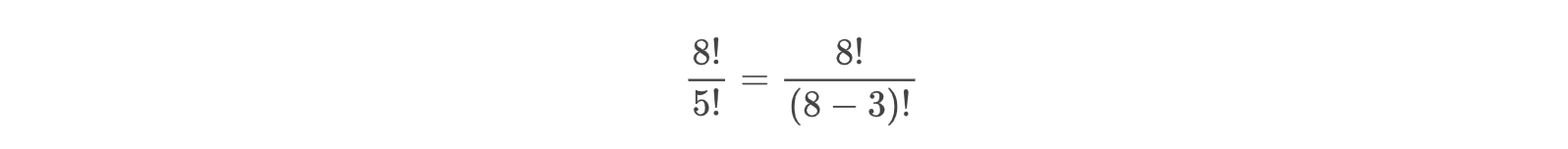
那么我现在有n个人,选出k个人进行排名,有多少种排列方式呢?
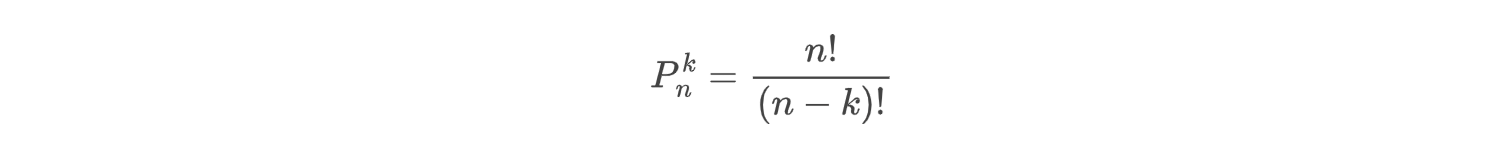
特别的:

组合问题:不关心顺序,一视同仁
仍然是8个人,现在不发奖牌,不排名,只是选出三个人,有多少种组合方式呢?
因为不关心顺序,所以选出的三个人是”ABC”、”ACB”、BAC”、”BCA”、”CBA”还是”CAB”我都不关心,这6种排序方式都归为同一种组合。所以我只要排序问题后面,把三个人的排序方式除掉就行了。
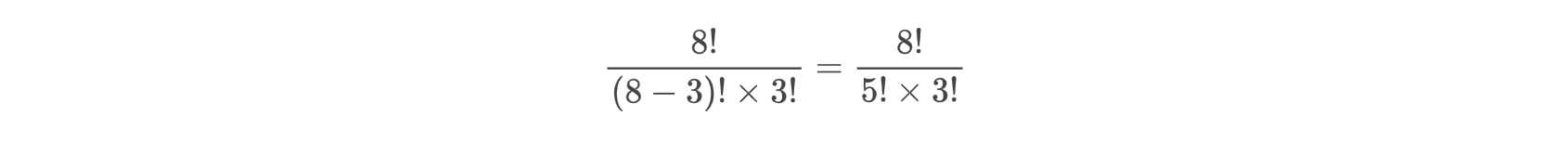
根据排列与组合之间的关系,组合问题就是去除掉排列问题中组合数量的排列关系
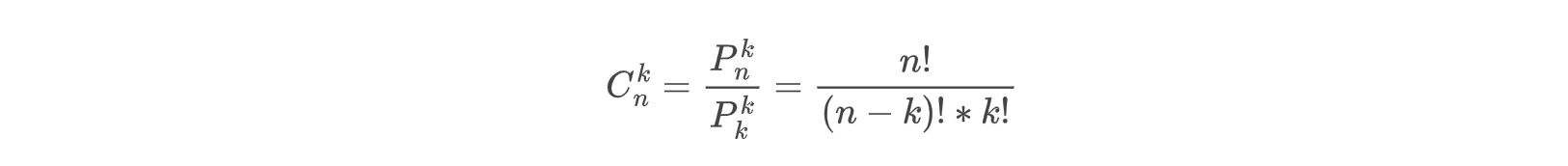
根据这个公式,我们也可以得到:
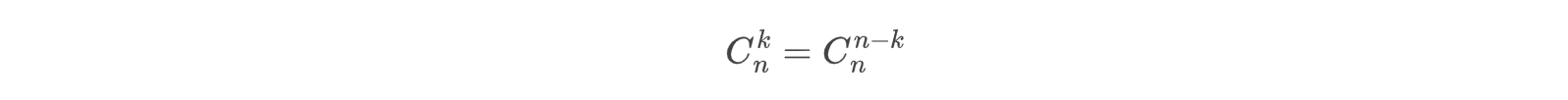
特殊的:
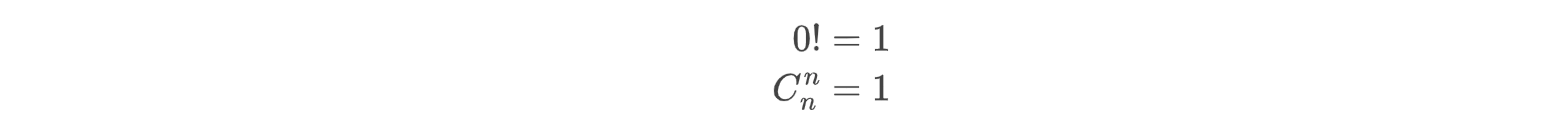
分组问题:多重排列组合
分组问题可以看成是多个组合问题
- 平均分组
6个人两两分组,有多少种组队方式呢?
因为都是两人组,这里不再关心分组的排列顺序,三个分组都是等价的,所以可以除去所有队伍数量的排列数
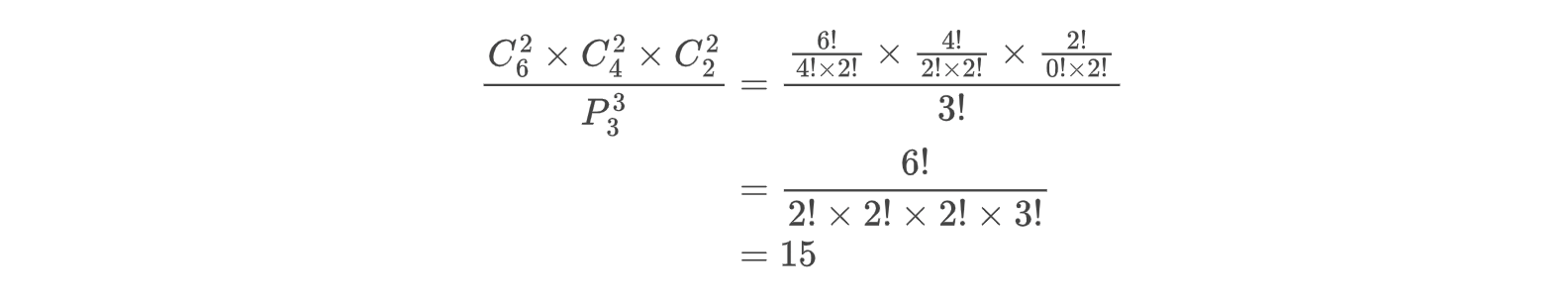
- 不平均分组
6个人分3组,各组人数分别为3人、2人、1人,共有多少分法?
因为三组数量不一样,所以选出的三组是有区别的,不能“一视同仁”。
但是先选1人还是先选3人,这个是无所谓的,这就跟排列问题类似,先给铜牌颁奖还是先给金牌颁奖是不会影响结果的。
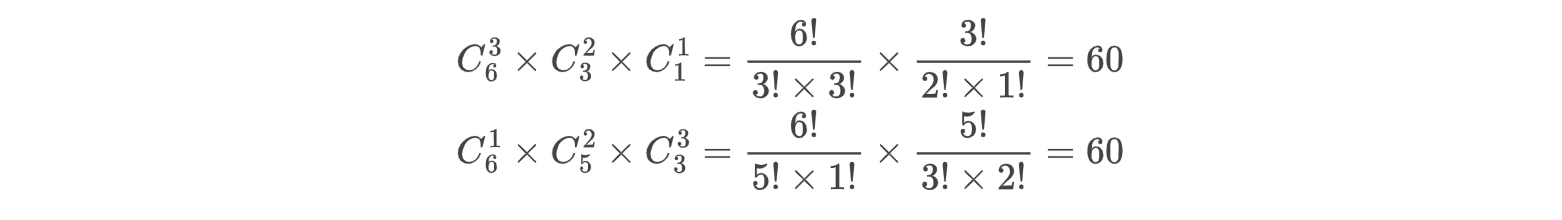
- 部分平均分组
6个人分成3组,各组人数分别为4人、1人、1人,共有多少种分法?
先用上面的逻辑思考一下,按照不平均分组的逻辑,这个应该有:
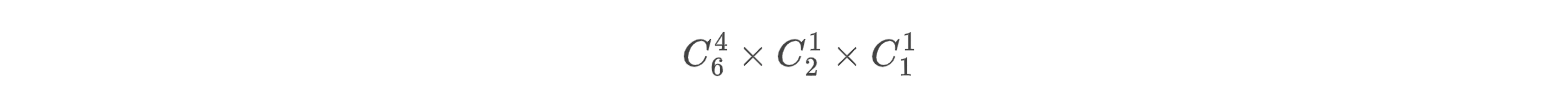
但是当我从6个人选出4个人之后,接下来的1个人分组是等价的,其实分组方式就已经确定的,不关心后面两个人分组的顺序,所以实际的结果应该是:
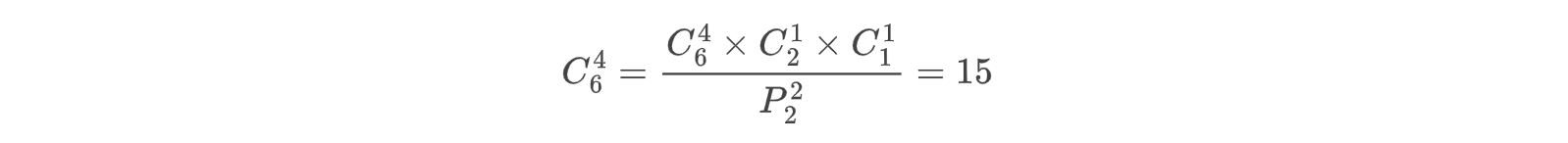
延伸思考:8个人分成3组,各组人数分别为4人、2人、2人,共有多少分法?
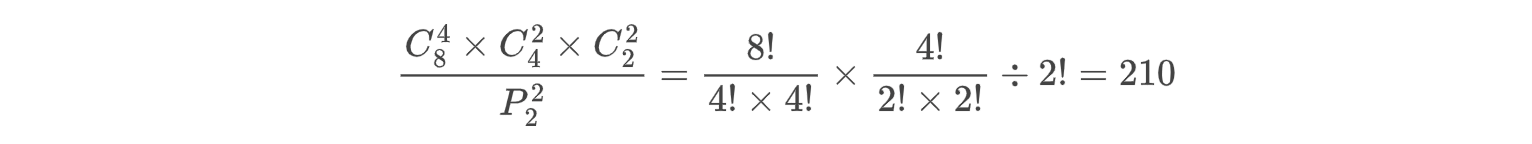
- 不定量分组
6个人分成3组,每组至少一个人,共有多少种分法?
这个问题需要把几种分组情况列出来:4,1,1、3,2,1、2,2,2。其中等分2,2,2分组相同。这实际是前三个问题的汇总。
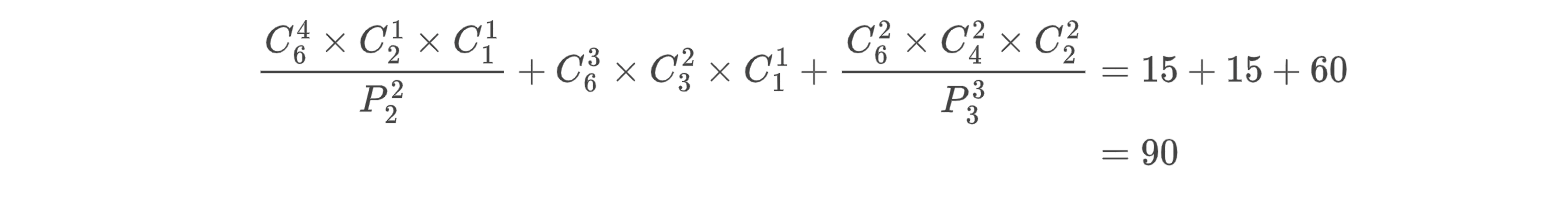
- 分配问题
6个人分成3组,每组至少一个人,然后3组分别被分配到一班、二班、三班,共有多少种分法?
此时这个问题就有排列问题了,也就是前面的结果再乘上一个3组的全排列:
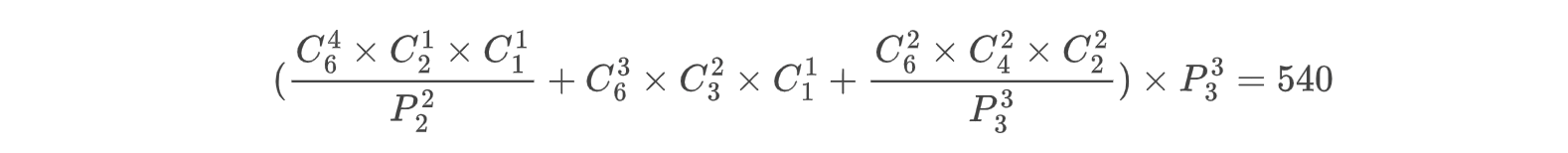
相同元素分组分配问题
分组问题
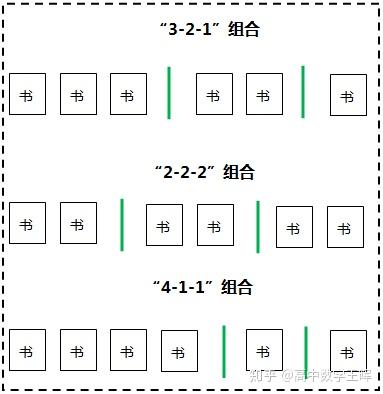
将6本相同的书分三组,每组至少有一本,共有多少种分法?
6本分成三组,每组至少一本,分组情况列出来:4,1,1、3,2,1、2,2,2。因为每本书相同,没有顺序关系,每种情况方式只有分法。所以总共也就3种分法。
分配问题
分配问题:将6本相同的书分给甲、乙、丙三个人,每个人至少一本,共有多少种分法?
这个有两种解法:
第一种思路:
6本分成三组,每组至少一本,分组情况列出来:4,1,1、3,2,1、2,2,2。分类讨论一下:

第二种思路:
因为每个人至少一本书,而且每本书都是一样的。所以先给甲、乙、丙各分一本书,这样就满足了每个人至少一本书的条件。然后就是讨论剩下的三本书的分配问题了:

- 隔板法:
6本书都是相同的,4,1,1、3,2,1、2,2,2三种分组都只有一种情况,但是分配给甲、乙、丙三个人就不一样了,比如下面的“4,1,1”这种分法:
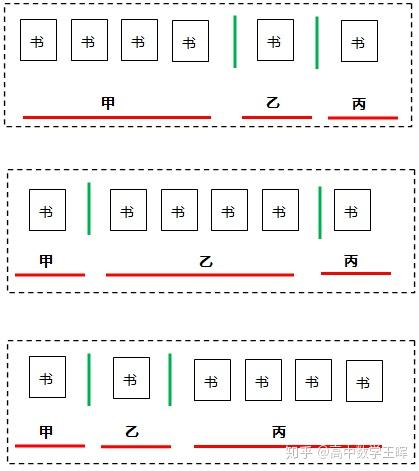
经上图启发,6本相同的书排成一排,因为每个人至少一本,也就是从6本书形成的5个空档中插入两个隔板。

分配问题:将6本相同的书分给甲、乙、丙三个人,共有多少种分法?
这个问题和上面的分配问题:将6本相同的书分给甲、乙、丙三个人,每个人至少一本,共有多少种分法?区别在于,有人可能分不到书。
这个用常规方法解题就复杂多了,分情况讨论一下:

如果用隔板法就简单多了:
结合一下上面分配问题:将6本相同的书分给甲、乙、丙三个人,每个人至少一本,共有多少种分法?问题的第二种常规解题思路和隔板法解题思路。
假设我有9本书分给甲、乙、丙三个人,每人至少一本,共有多少种分法?是不是就是每个人至少分一本,然后考虑6本书怎么分配给甲、乙、丙三个人。所以这个将6本相同的书分给甲、乙、丙三个人,共有多少种分法?和9本书分给甲、乙、丙三个人,每人至少一本,共有多少种分法?这两个问题结果上是一样的。那9本书用隔板法进行分配就有
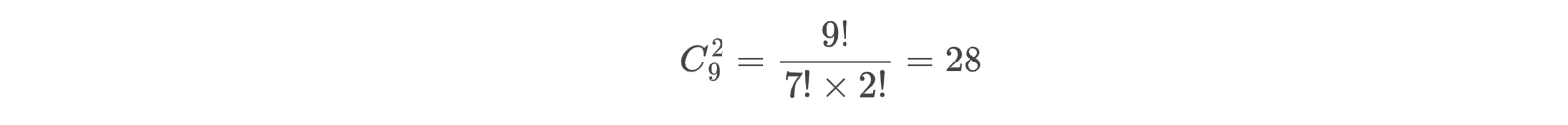 |
|