几何、拓扑、分析综合第三篇——同调论

天策大將軍

1.同调论的背景

今天我们就来来谈谈几何中的同调论 , 事实上代数拓扑 , 微分几何 , 代数几何与复几何等方向的许多问题的研究进展都和同调论的发展有关 , 而其中一项贡献就是把 Gauss-Bonnet 定理和 Riemann-Roch 定理联系起来 , 事实上同调代数和代数拓扑几乎是一起发展起来的 , 于是我们就先讨论代数拓扑的起源—— konigsberg 七桥问题 .
问题描述如下：konigsberg 市区一共有七座桥将陆地和岛屿连接在一起 , 将七座桥进行编号为 1,2,…,7 , 如下图所示 , 问一个人能否找到一个方法使得他无重复地走遍这七座桥 , 即每座桥只能经过一次？接下来我们将图中的陆地和岛屿在自身情况下收缩为一个点(即用拓扑的方法进行变形)后得到四个点 , 同时将每一座桥变形为某两个点之间的连线 , 这样就得到了一个网络图 , 这便是小学生都熟知的一笔画问题 , 易知由于图上的四个点皆是其实顶点(即与该点相连的连线的条数为奇数) , 故该图不能一笔画成 , 因此七桥问题无解 .


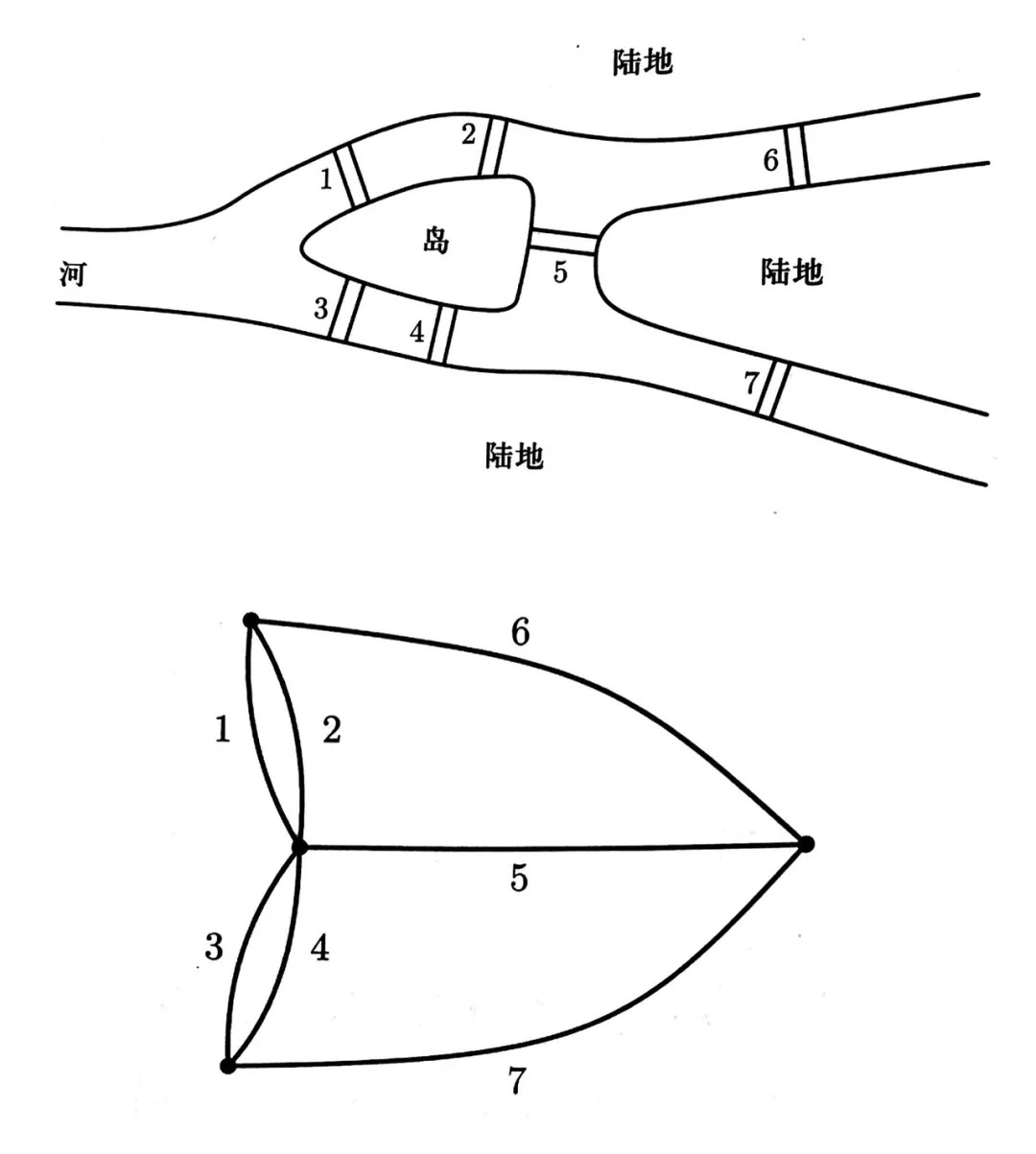
事实上 , 一个图形或空间的 Euler 数是根据对某个图形或空间的单纯剖分进行计算的 , 即先分别计算各个维数的单形个数 , 再取交错和就得到了 Euler 数 , 而 Euler 数并不依赖于剖分的选取 , 故能反映图形或空间自身的某种性质 , 于是上述七桥问题是否可解就与对应的网络图中奇顶点的个数有关 , 而至多有两个奇顶点的网络图才是可解的 , 否则不可解 , 进而奇顶点的个数和 Euler 数一样都能反映图形或空间的某种特征 , 如果只是将图形放大或压缩 , 而不撕破 , 那么奇顶点的个数和欧拉数都是不变的 , 这种性质就成为拓扑性质 , 它是与图形的大小 , 夹角和歪曲程度无关的性质 , 在这之前的古典几何学只研究图形的大小 , 面积 , 夹角 , 弯曲度等度量性质 , 那么现在加入拓扑性质后 , 就产生了新的拓扑学问题 , 如闭曲面的分类 , 单侧曲面(如 Mobius 带) 以及地图着色问题等 , 后来 1899 年 Poincaré 发表了一篇文章 , 在定义了 Betti 数的基础上提出了利用剖分来计算 Betti 数的方法后 , 代数拓扑学才真正意义上发展秋来 , 其实 Poincaré 的这篇文章奠定同调论基础的文章 , 因此代数拓扑和同调论几乎是同时兴起的 . 随后他又接连发表了五篇文章作为补充 , 提出了 Euler-Poincaré 公式 , 即把 Euler 数(各个维数的单形个数的交错和)表示为各维单形的 Betti 数的交错和 , 这使得 Euler 数在同调意义下有了新的解释 , 因此它将 Gauss-Bonnet 公式和 Riemann-Roch 公式联系起来 .
同调的概念最早出现在 Riemann 的关于复变函数的文章中 , 在一个曲面 M 上 , 同调就是 M 上闭曲线的一种分类 , 或者是闭曲线几何中的一个等价类 \sim , 对于任意闭曲线 x,y,z , 如果构成等价类则需满足下面的三条性质
(i) 自反性 , 即 x \sim x ;
(ii) 对称性 , 即若 x \sim y , 则 y \sim x ;
(iii) 传递性 , 即若 x \sim y 和 y \sim z , 则 z \sim z ;
于是 x 同调于 y 就理解为 x,y 是 M 上的两条闭曲线 , 且在 M 上存在一个二维区域 \sigma , 使得 x 和 y 构成 \sigma 的边界 , 记作 x \sim y .
上面定义同调的方式极其粗糙 , 故我们先来讨论另一种分类法——同伦 , 如果一条闭曲线是连续映射 \alpha: \mathbb{S}^1 \to M , 其中 \mathbb{S}^1=\{(x,y) \in \mathbb{R}^2~|~x^2+y^2=1\} , 则可以定义同伦 . 设 \alpha,\beta:\mathbb{S}^1 \to M 是 M 上的两个连续映射或两条闭曲线 , 如果存在一个连续映射 F:\mathbb{S}^1 \times [0,1] \to M , 使得 F|_{\mathbb{S}^1 \times \{0\}}=\alpha: \mathbb{S}^1 \to M 和 F|_{\mathbb{S}^1 \times \{1\}}=\beta: \mathbb{S}^1 \to M 成立 , 则称 \alpha 与 \beta 同伦 , 记作 \alpha \simeq \beta , 其中 [0,1] 是闭区间 . 引入同伦的动机是可以和同调对照起来作比较 , 可以更深刻地理解同调 , 而在 Riemann 的工作中并没有定义同伦 , 关于同伦论也是后来 Poincaré 加进去的 , 事实上 Riemann 关于同调只提出了连通阶数 , 他用连通阶数直接对曲面进行拓扑分类 , 这个连通阶数和曲面的亏格有关 , 另外同调的粗浅概念也仅用于曲线积分的计算 , 在分析学中常用曲线积分的积分限来对闭曲线进行研究 , 在证明经典的 Riemann-Roch 时就利用了积分 I(u,\gamma)=\displaystyle\int_{\gamma}-\frac{\partial u}{\partial y}dx+\frac{\partial u}{\partial x}dy , 为了方便讨论将上面的积分简记为全纯微分式的积分 \displaystyle\int_{\gamma}\omega , 于是得到了两条闭曲线上的积分相等的充要条件就是两条闭曲线同调 .
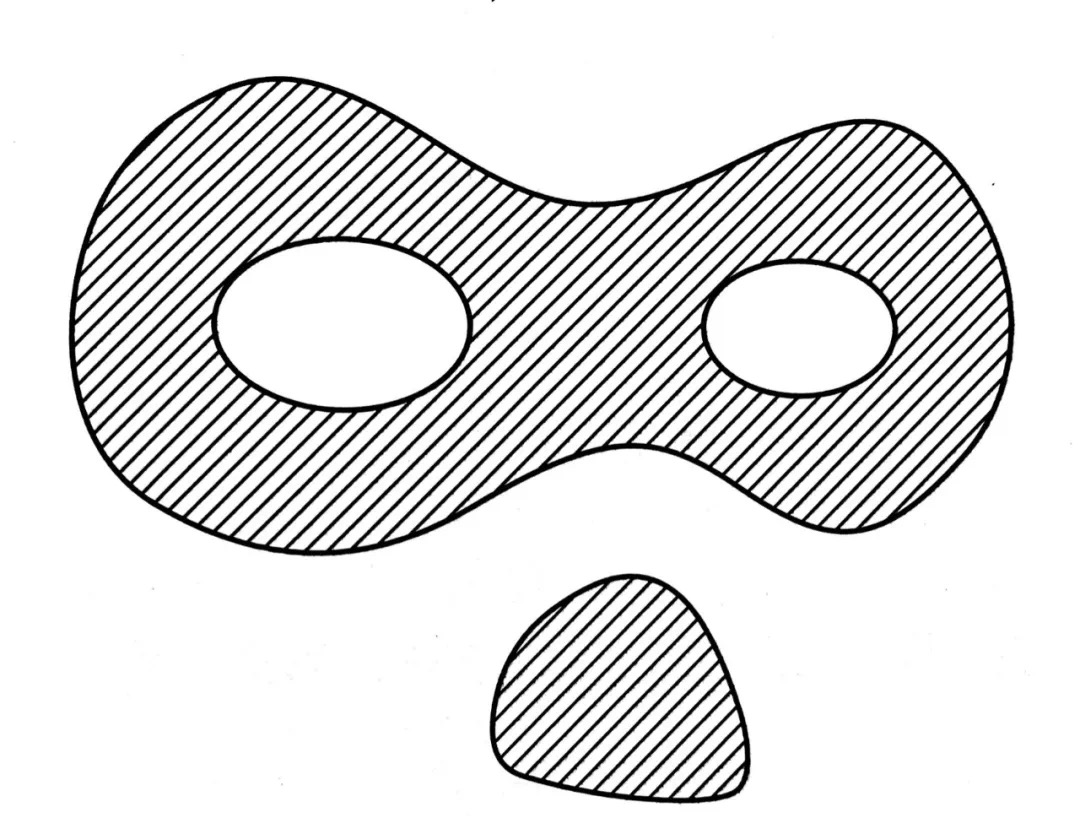
从上面的讨论可知 , 同调比同伦更能直接说明一些数学现象 , 这就能解释同调比同伦出现的早的原因 . 下面我们来考察一次微分式的积分 \displaystyle\int_{\gamma}\omega , 在一个复坐标 z 的邻域内 , 一次微分式 \omega 表示为 f(z)dz , 其中 f(z) 是全纯或半纯的复值函数 , 如果 f(z) 全纯或半纯 , 则称 f(z)dz 是全纯微分式或半纯微分式 , 设 \Omega 是复平面上的一个区域(可以有洞 , 也可以不连通) , 甚至可以是 Riemann 面 , 如下图所示 .


而 \Omega 中的一条道路是映射 \gamma:[0,1] \to \Omega , 如果 \gamma(0)=\gamma(1) , 则称 \gamma 为闭道路 , 在 \Omega 的一个局部坐标 z 下 , 微分式表示为 \omega=f(z)dz , 于是一条道路在某一坐标邻域内表示为 \gamma(t)=x(t)+iy(t) , 其中 z=x+iy 是局部坐标 , 如果 \Omega 是 Riemann 面 , 只需假定 \Omega 的像集为 \gamma([0,1]) 即可 , 接下来令 f(\gamma(t))=u(t)+iv(t) , 则可以定义曲线积分 \displaystyle\int_{\gamma}\omega=\int_{\gamma}f(z)dz=\int_0^1(u(t)+iv(t))(x'(t)+iy'(t))dt=\int_0^1(u(t)x'(t)-v(t)y'(t))+i\int_0^1(v(t)x'(t)+u(t)y'(t))dt\\进而得到上面的积分与复坐标 z 的选取无关 . 故对于像集不在某个坐标邻域内的道路 \gamma' , 则可以将 \gamma' 分成几段首尾相连且像集在坐标邻域中的道路 , 再利用上面的方法定义曲线积分 , 最后求和得到 \gamma' 上的积分 .
设 \gamma:[0,1] \to \Omega 是其中一条道路且 \Gamma(\Omega) 是 \Omega 上所有分段 C^{\infty} 的闭道路构成的集合 , 因此在 \Gamma(\Omega) 中就可以得到一个等价类 \sim , 即若 \gamma_1,\gamma_2 \in \Gamma(\Omega) 且 \gamma_1 \sim \gamma_2 , 则对 \Omega 中的任意全纯 1-形式 \omega 有 \displaystyle\int_{\gamma_1}\omega=\int_{\gamma_2}\omega , 称 \sim 为同伦等价类 , 之前定义的同伦是考虑闭道路 \gamma:\mathbb{S}^1 \to \Omega 的同时保证 \gamma 连续即可 , 那么现在考虑闭道路 \gamma':[0,1] \to \Omega 且满足 \gamma'(0)=\gamma'(1) , 同时需要保证 \gamma' 分段 C^{\infty} , 但这两者对于曲线积分 \displaystyle\int_{\gamma}\omega 没有本质差别 , 事实上可以将 \gamma' 写为 \gamma:\mathbb{S}^1 \to \Omega , e^{i2\pi\theta} \mapsto \gamma'(\theta) , 因此关于道路的可微性就是适当加一些条件后然后考虑曲线积分即可 .
首先我们根据下面的一个引理来说明同伦的等价类可以保证曲线积分相等 .
引理：设 \gamma_1,\gamma_2:[0,1] \to \Omega 是两条闭道路 , 即满足 \gamma_1(0)=\gamma_1(1) 和 \gamma_2(0)=\gamma_2(1) ，且这两条闭道路具有适当的可微性 , 再令 F:[0,1] \times [0,1] \to \Omega 是连接 \gamma_1,\gamma_2 的闭道路同伦 , 即有 F|_{[0,1] \times \{0\}}=\gamma_1 和 F|_{[0,1] \times \{1\}}=\gamma_2 , 以及 \,\forall\,t \in [0,1] , F 满足 F(0,t)=F(1,t) , 则对任意的全纯微分式 \omega , 有 \displaystyle\int_{\gamma_1}\omega=\int_{\gamma_2}\omega .
证明：当 \gamma(t)=x(t)+iy(t) 时 , 有 \gamma'(t)=x'(t)+iy'(t) , 于是得到 \begin{align*} \int_{\gamma_2}\omega-\int_{\gamma_1}\omega&=\int_0^1f(\gamma_2(t))\gamma'_2(t)dt-\int_0^1f(\gamma_1(t))\gamma'_1(t)dt\\&=\int_0^1f(F(t,1))F_t(t,1)dt-\int_0^1f(F(t,0))F_t(t,0)dt\\&=\int_0^1ds \cdot \frac{\partial}{\partial s} \left[ \int_0^1f(F(t,s)\cdot F_t(t,s))dt \right]\\&=\int_0^1ds\left[ \int_0^1(\frac{\partial}{\partial z}(F(t,s))\cdot F_s(t,s)\cdot F_t(t,s)+f(F(t,s))F_{ts}(t,s))dt \right]\\&=\int_0^1dt\int_0^1\left[ \frac{\partial f(F(t,s))}{\partial t}\cdot F_s(t,s)+f(F(t,s))\frac{\partial}{\partial t}F_s(t,s) \right]ds\\&=\int_0^1dt \cdot \frac{\partial }{\partial t}\left[ \int_0^1f(F(t,s))F_s(t,s)ds  \right] \end{align*}\\其中 F_t=\displaystyle\frac{\partial F}{\partial t} 和 F_s=\displaystyle\frac{\partial F}{\partial s} , 由于 F(0,s)=F(1,s) 和 F_s(0,s)=F_s(1,s) , 故上式的结果为零 , 因此引理得证 .
由于 \omega=f(z)dz 是全纯微分 , 故有 \displaystyle\frac{\partial}{\partial t}f(F(t,s))=\frac{\partial}{\partial z}(F(t,s))\cdot F_t(t,s)\\ \displaystyle\frac{\partial}{\partial s}f(F(t,s))=\frac{\partial}{\partial z}(F(t,s))\cdot F_s(t,s)\\ 其中 \displaystyle\frac{\partial f}{\partial z} 是全纯函数 f(z) 的导数 , 令 f(z)=u(x,y)+iv(x,y) , 则根据 Cauchy-Riemann 条件 \displaystyle\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y} 和 \displaystyle\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x} , 于是有 \displaystyle\frac{\partial f}{\partial z}=\lim\limits_{\Delta z \rightarrow 0}\frac{f(z+\Delta z)-f(z)}{\Delta z}=\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x} , 若 F(t,s)=x(t,s)+iy(t,s) , 则有
\begin{align*} \frac{\partial}{\partial t}f(F(t,s))&=\frac{\partial}{\partial t}\left( u(x(t,s),y(t,s))+iv(x(t,s),y(t,s)) \right)\\&=\frac{\partial u}{\partial x}\cdot\frac{\partial x}{\partial t}+\frac{\partial u}{\partial y}\cdot\frac{\partial y}{\partial t}+i\frac{\partial v}{\partial x}\cdot\frac{\partial x}{\partial t}+i\frac{\partial v}{\partial y}\cdot\frac{\partial y}{\partial t}\\&=\left( \frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x} \right)\frac{\partial x}{\partial t}+\left( \frac{\partial u}{\partial y}+i\frac{\partial v}{\partial y} \right)\frac{\partial y}{\partial t}\\&=\left( \frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x} \right)\frac{\partial x}{\partial t}+\left(-\frac{\partial v}{\partial x}+i\frac{\partial u}{\partial x} \right)\frac{\partial y}{\partial t}\\&=\left( \frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x} \right)\left( \frac{\partial x}{\partial t}+i\frac{\partial y}{\partial t} \right)\\&=\frac{\partial f}{\partial z}\cdot F_t \end{align*}\\
同理有 \displaystyle\frac{\partial}{\partial s}f(F(t,s))=\frac{\partial f}{\partial z}\cdot F_s , 故上面两个等式的证明依赖于 f(z) 的全纯性 , 因此引理成立的条件就是 \omega 全纯 , 即在同伦等价的关系下 , 全纯微分式的积分不变 .
下面我们给出 Cauchy 定理 , 然后再与上边的引理进行比较来说明引入同调是极其自然的 .
Cauchy 定理：设 \Omega 是复平面中的区域 , 且 \sigma 是 \Omega 中的一个圆盘或多边形 , 令 \partial \sigma 是 \sigma 的有向边界且使得沿着 \partial \sigma 运动时 , \sigma 总是在左侧 , 若 f(z) 是 \Omega 上的全纯函数 , 则有 \displaystyle\int_{\partial \sigma}f(z)dz=0 , 其中 \partial \sigma 是一条闭道路 .
事实上在上边的 Cauchy 定理中 , \partial \sigma 是一条有向闭曲线 , 则存在一串分段可微映射 \gamma_i:[0,1] \to \Omega~,~i=1,2,…,n , 使得 \,\forall\,i=1,2,…n-1 , 有 \gamma_i(1)=\gamma_{i+1}(0) 和 \gamma_n(1)=\gamma_1(0) , 同时用 \gamma_1 \ast \gamma_2 \ast … \ast \gamma_n 表示 \gamma_1,\gamma_2,…,\gamma_n 首尾相连构成的有向闭曲线 , 当 \partial \sigma=\gamma_1 \ast \gamma_2 \ast … \ast \gamma_n 时 , 有 \displaystyle\int_{\partial \sigma}f(z)dz=\sum_{i=1}^n\int_{\gamma_i}f(z)dz , 由于在 \Omega 中有整体的坐标 z , 故上面的等式左边可以直接定义为全纯函数 f(z) 在区域 \Omega 内沿路径 \partial \sigma 的曲线积分 , 但如果 \Omega 是 Riemann 面上的区域 , 此时 \Omega 可能没有整体坐标 , 且上面等式的左边写作 \displaystyle\int_{\partial \sigma}\omega , 但它不能直接定义 , 因此只能通过上面等式的右边来定义 , 于是取 \gamma_i 的像集在坐标邻域内且右边的积分结果与 \gamma_i 的取法无关 , 这就是前面提到的道路的同伦等价 .
然后我们讨论的问题是如何从 Cauchy 定理出发去得到不同于同伦等价关系的关于同调的概念 , 于是不妨先采用下面的定义 , 即如果对于 \Omega 中的任意全纯微分式 \omega 总有 \displaystyle\int_x\omega=\int_y\omega , 则称两条闭曲线 x,y 在 \Omega 中同调 , 这个定义也不是同调的真正定义 , 但可以作为用全纯微分式在闭曲线上的积分作为定义同调的动机 , 事实上要定义同调必须要阐述清楚闭曲线 , 面块(圆盘或多边形) , 边界这些概念 . 根据上面讨论可知 , 由于曲线作为积分限 , 故闭曲线是集合 c=\{\gamma_i:[0,1] \to \omega~|~i=1,2,…,n\} 且满足 \displaystyle\sum_{i=1}^n(\gamma_i(1)-\gamma_i(0))=0 , 而面块则是保证等式 \displaystyle\int_{c_1}\omega=\int_{c_2}\omega 成立的一种几何体 , 根据 Cauchy 定理可知 , 设 C_1(\Omega) 是集合 \{\gamma:[0,1] \to \Omega\} 张成的无穷维线性空间 , 则得到 c_1-c_2=\displaystyle\sum_i\partial \sigma_i , 进而有 \displaystyle\int_{c_1}\omega=\int_{c_2}\omega+\sum_i\int_{\partial \sigma_i}\omega , 又由于上式中的 \displaystyle\sum_i\int_{\partial \sigma_i}\omega=0 , 因此 \displaystyle\int_{c_1}\omega=\int_{c_2}\omega , 至此为止我们就可以来定义同调的概念了 .
设 c=\{\gamma_i:[0,1] \to \omega~|~i=1,2,…,n\}=\displaystyle\sum_{i=1}^n\gamma_i , 若满足 \displaystyle\sum_{i=1}^n(\gamma_i(1)-\gamma_i(0))=0 , 则称道路 c 为闭道路或闭链 , 令 c_1 和 c_2 是 \Omega 中的两个闭链 , 如果存在 \displaystyle\sum_i\sigma_i , 使得 c_1-c_2=\displaystyle\sum_i\partial \sigma_i 成立 , 则称 c_1 同调于 c_2 . 然后就可以来说明同调和同伦的区别 , 考察下图


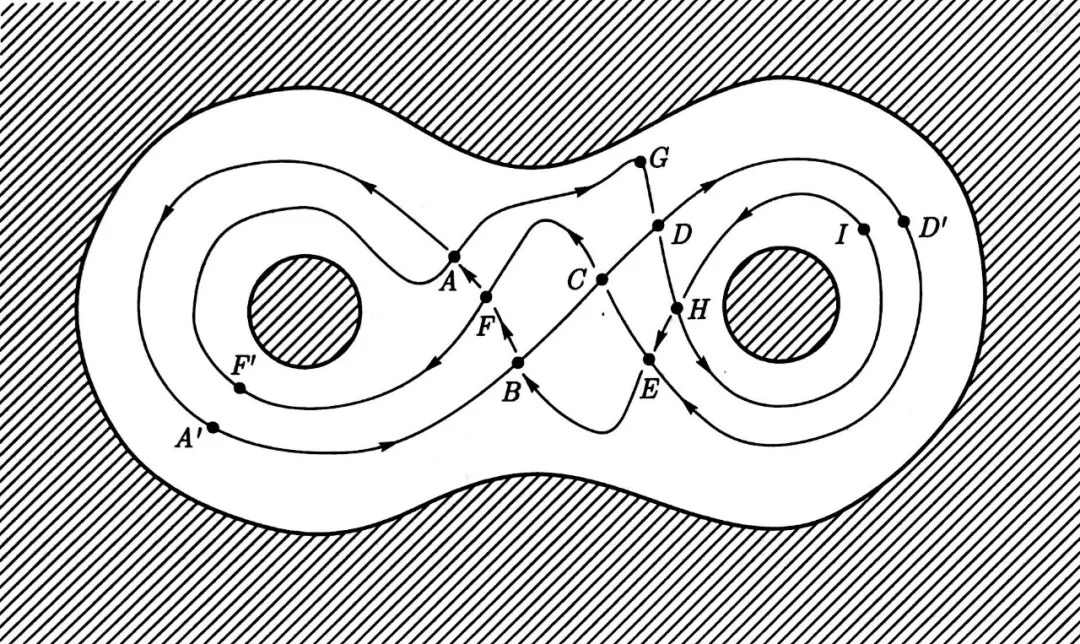
一条同伦意义下的闭道路 \alpha:\mathbb{S}^1 \to \Omega 在上图中表示为从 A 点出发 , 依次经过 G,D,H,I,E,B,F,A',B,C,D,D',E,C,F,F' , 再回到 A 点的回路 , 故 \alpha 不同论于零 , 即不存在一个映射 F:\mathbb{S}^1 \times [0,1] \to \Omega 使得 F|_{\mathbb{S}^1 \times \{0\}}=\alpha 且将 \mathbb{S}^1 \times \{1\} 映射为一个点 , 但如果把 \alpha 视为同调意义下的闭链 , 即将闭道路分割为由若干段收尾相连的线段组成的闭链 , 则得到
\begin{align*} \alpha&=\partial[\left< AA'BFF'A \right>+\left< FAGDCF \right>+\left< BCEB \right>+\left< DD'EHD \right>+2\left< ECDHE \right>]\\&=\partial\left< AA'BFF'A \right>+\partial\left< FAGDCF \right>+\partial\left< BCEB \right>+\partial\left< DD'EHD \right>+2\partial\left< ECDHE \right> \end{align*}\\
如果将上面的等式两边都重新分成若干小段然后再重新排列 , 可以使得等式两端完全相同 , 则 \alpha 同调于零 , 故对于闭道路的分类 , 同调的分类比较粗糙 , 进而得到彼此同伦的闭道路必同调 , 这就是在同调意义下的闭道路可以分段重排的原因 .
下面根据 Cauchy 定理来讨论上面等式中各个符号的意义 , 设 \sigma 是复平面上的圆盘或多边形 , \partial \sigma 是一条闭道路且沿该道路运动时 \sigma 总是在左边 , 故如果 \partial \left< AA'BFF'A \right> 中的 \left< AA'BFF'A \right> 看作沿闭道路 A \to A' \to B \to F \to F' \to A 围成的曲多边形 \sigma , 此时 \partial \left< AA'BFF'A \right>=\partial \sigma , 如果闭道路 B \to C \to E \to B 围成的曲多边形为 \tau , 则 \partial \tau 应该定义为 \partial \tau=B \to C \to E \to B=BC+CE+EB , 因此在计算 \partial\left< AA'BFF'A \right> , \partial\left< FAGDCF \right> , \partial\left< BCEB \right> , \partial\left< DD'EHD \right> 和 \partial\left< ECDHE \right> 时就会区别 , 即在 Cauchy 定理中 \sigma 是几何多边形 , 而在曲面上 \left< AA'BFF'A \right> , \left< FAGDCF \right> , \left< BCEB \right> , \left< DD'EHD \right> 和 \left< ECDHE \right> 都是定向多边形 , 故得到 \left< BCEB \right>=\left< CEBC \right>=\left< EBCE \right>=-\left< BECB \right> , 因此就得到了曲线上闭道路的同调分类方法 .
Riemann 在他的工作中指出同调的概念是根据连通阶数来表示的 , 连通阶数的定义为如果在具有边界的曲面 F 上能作出 n 条闭曲线 \alpha_1,\alpha_2,…,\alpha_n , 其中这些闭曲线各自单独或集体都不能把曲面 F 分割成两块 , 而任何 n+1 条闭曲线必能把 F 分割为两块及以上 , 则称这个曲面是 n+1 阶连通曲面或曲面的连通阶数为 n+1 , 如环面 \mathbb{T}^2 的连通阶数为 3 . 事实上 Riemann 还对连通阶数在几何上进行讨论 , 即沿着一条横剖线剪开曲面就可以把 n+1 阶连通曲面变成 n 阶连通曲面 , 故当减了 n 次后曲面就变成了多边形 , 即多边形的连通阶数为 1 .
Betti 在高维图形中引入连通阶数的概念 , 即得到了 n 维图形中从 1 维到 n-1 维的各个维数的连通阶数 , 具体的定义如下：高维图形上能作出若干个闭曲面 , 而它们集体也无法成为这个图形的任何三维区域的边界 , 这种闭曲面的最大个数就定义为二维连通阶数等等……事实上 Betti 还计算量一些四维图形的连通阶数 , 直到后来连通阶数被 Poincaré 重新定义 , 即连通阶数减 1 就被称为 Betti 数 , 而 Betti 数和曲面的同调类分类密切相关 , 因此对于一个曲面上存在闭道路 \gamma_1,\gamma_2,…,\gamma_n 使得任意的 \displaystyle\sum_{i=1}^nc_n\gamma_n 不同调于零 , 且对于任意闭道路 \gamma , 存在某个 \displaystyle\sum_{i=1}^nc_n\gamma_n , 使得 \gamma 同调于 \displaystyle\sum_{i=1}^nc_n\gamma_n , 此时 n 就是一维 Betti 数 , 而  \displaystyle\sum_{i=1}^nc_n\gamma_n 是 \gamma_1,\gamma_2,…,\gamma_n 的线性组合且 c_i~(i=1,2…n) 是常数 .
最后我们给出一个断言 , 设 M 是亏格为 g 的闭紧致 Riemann 面 , 且在该 Riemann 面上有 2g 个封闭道路 \gamma_1,\gamma_2,…,\gamma_{2g} 使得 I(u,\gamma_1)=I(u,\gamma_2)=…=I(u,\gamma_{2g})=0 成立 , 则对于一切封闭道路 \gamma , 有 I(u,\gamma)=0 , 以及 M 的 Betti 数是 2g .
2.同调群与 Betti 数

Poincaré 在1899年发表的一篇文章宣告了代数拓扑学的诞生 ,该文借助空间的剖分来阐述高维同调的含义 , 同时也给出 Betti 数的组合算法和根据同调的概念来引入同调群 . 本文先讨论同调群 , 然后再讨论 Betti 数的算法 .
空间的一个剖分是将空间分成若干个基本图形之和 , 这些基本图形是各个维数的单形的同胚像 , 一个 n 维单形可以看组一个 n 维三角形 , 如零维单形是一个点 , 一维单形是一条线段 , 二维单形是一个三角形 , 三维单形是一个四面体…… n 维单形是一个具有 n+1 个顶点的广义四面体 , 且一个单形的边界是一些低维单形之和 , 每一个低维单形称为原单形的一个面 . 对于空间的每一个剖分 , 有规则如下 :
(i) 空间是有限个单形之和 ;
(ii) 如果任何两个单形相交 , 则这两个单形的交也是一个单形 , 即公共面 ;
事实上空间的许多性质是可以通过剖分的组合结构得到 , 于是称有限个单形的集合 K 为一个剖分的组合结构 , 且满足
(i) 若单形 \sigma \in K , 则 \sigma 的所有的面均属于 K ;
(ii) 若任意两个单形 \sigma,\tau \in K , 则有 \sigma \cap \tau \in K ;
则称一个剖分的组合结构 K 为一个单纯复形 , 设 K 的所有零维单形为 a_1,a_2,…,a_N , 因为 K 中的每一个单形都可以由它的顶点 (零维单形) 唯一确定 , 故 K 中的每一个单形是零维单形集的一个子集 (a_{i_1},a_{i_2},…,a_{i_n}) , 其中 a_{i_1},a_{i_2},…,a_{i_n} 的顺序变化只代表同一个子集合 (单形) , 故只要根据上述的子集合来列出 K 中的所有单形就能确定 K .
根据上面的讨论可知 , 空间上的同调可以用空间的剖分所给出的单纯复形来定义 , 前面我们从 cauchy 定理中积分限的性质来给出同调的概念 , 那么积分限可以视为单形的线性组合 , 接下来只需要说明定向的概念即可 , 事实上关于之前所定义的定向多边形不易推广到高维情形 , 毕竟在高维情形下边界 \partial 的走向定义较为困难 , 由于三角形的定向可以理解为顶点的一个排列且相差一个偶置换的两个排列的定向是相同的 , 故三角形的定向可以很自然地推广到一切单形 , 这也是 Poincaré 选择单形作为基本图形来剖分空间的原因 .
下面给出定向单形的定义 , 对于每一个单形 (a_{i1},a_{i2},…,a_{in}) 的顶点的一个排列代表单形的一个定向 , 相差一个偶置换的两个排列表示同一定向 , 相差一个奇置换的两个排列表示不同定向 , 故顶点的排列 a_{i_1},a_{i_2},…,a_{i_n} 确定单形 (a_{i_1},a_{i_2},…,a_{i_n}) 的定向 , 得到的定向单形记作 \left< a_{i_1},a_{i_2},…,a_{i_n} \right> , 进而可知一个单形恰好有两个定向 , 但如果这个单形是零维的 , 则还需要对定向的定义进行补充 , 由于零维单形是一个点 a , 故不可能用顶点的排列来表示定向 , 因此只能采用 +a 或 -a 来定义零维单形的定向 , 于是令 \sigma 为一个单形 , 则它的定向单形为 \overrightarrow{\sigma} 或 \overleftarrow{\sigma} , 然后我们就可以定义单纯复形的同调群了 .
定义：设 K 是一个单纯复形 , 则有
(i) K 中的 k 维定向单形的线性组合 c_1\overrightarrow{\sigma_1}+c_2\overrightarrow{\sigma_2}+…+c_l\overrightarrow{\sigma_l} 称为一个 k 维链 , 其中 c_1,c_2,…,c_l 是实数 和 \overrightarrow{\sigma_1},\overrightarrow{\sigma_2},…,\overrightarrow{\sigma_l} 是 k 维定向单形 , 对于 k 维链规定 c\overrightarrow{\sigma}=-c\overleftarrow{\sigma} , 其中 c 是任意的实数和 \sigma 是任意的 k 维单形 .
(ii) k 维链构成的集合为 C_k(K,\mathbb{R}) , 而 C_k(K,\mathbb{R}) 是一个实向量空间且维数等于单纯复形 K 中 k 维单形的个数 .
(iii) 由定向单形的边缘链 \partial\left< a_{i_0}a_{i_1}…a_{i_k} \right>=\displaystyle\sum_{s=0}^k(-1)^s\left< a_{i_0}a_{i_1}…\widehat{a_{i_s}}…a_{i_k} \right> 诱导出线性空间的同态 \partial:C_k(K,\mathbb{R}) \to C_{k-1}(K,\mathbb{R}) , 其中 \widehat{a_{i_s}} 表示在定向单形 \left< a_{i_0}a_{i_1}…a_{i_k} \right> 中不出现顶点 a_{i_s} , 于是可以根据边缘链的定义得到 \partial^2=0 .
(iv) 单纯复形 K 的 k 维闭链群为 Z_k(K,\mathbb{R})=\{\alpha \in C_k(K,\mathbb{R})~|~\partial\alpha=0\} , 单纯复形 K 的 k 维边缘链群为 B_k(K,\mathbb{R})=\partial C_{k+1}(K,\mathbb{R}) , 以及单纯复形 K 的 k 维同调群为 H_k(K,\mathbb{R})=\displaystyle\frac{Z_k(K,\mathbb{R})}{B_k(K,\mathbb{R})} .
如果 K 是空间 M 上的一个剖分所给出的单纯复形 , 则 M 的 k 维 Betti 数就是 \dim H_k(K,\mathbb{R}) , 尽管这不是 Poincaré 关于 Betti 的组合算法 , 毕竟当时没有引入同调群 H_k(K,\mathbb{R}) 作为工具 , 但可以根据边缘算子 \partial 来计算 Betti 数 , 直到 1915 年 J.W.Alexander 用 Betti 数的拓扑不变性证明 Poincaré 计算的 Betti 数恰好是 \dim H_k(K,\mathbb{R}) 和 H_k(K,\mathbb{R}) 和 \dim H_k(K,\mathbb{R}) 不依赖于空间 M 的剖分 K 的选取 , 于是就得到了下面的 Poincaré 定理 .
Poincaré 定理: 设 K 是一个单纯复形且 n_k 表示 K 中 k 维单形的个数 , 则 K 的 Euler 数为 \displaystyle\sum_{k \geq 0}(-1)^kb_k , 其中 b_k 是 K 的 k 维 Betti 数 , 即 b_k=\dim H_k(K,\mathbb{R}) , 进而得到 \displaystyle\sum_{k \geq 0}(-1)^kn_k=\sum_{k \geq 0}(-1)^kb_k .
证明：由于 n_k=\dim C_k(K,\mathbb{R}) 和 b_k=\dim H_k(K,\mathbb{R}) , 且有 H_k(K,\mathbb{R})=\displaystyle\frac{Z_k(K,\mathbb{R})}{B_k(K,\mathbb{R})} , 故 \dim H_k(K,\mathbb{R})=\dim Z_k(K,\mathbb{R})-\dim B_k(K,\mathbb{R}) , 又由于 C_k(K,\mathbb{R}) \xrightarrow{\partial} B_{k-1}(K,\mathbb{R}) 是满同态且有 \partial^{-1}(0)=Z_k(K,\mathbb{R}) , 于是得到同构 \displaystyle\frac{C_k(K,\mathbb{R})}{Z_k(K,\mathbb{R})} \simeq B_{k-1}(K,\mathbb{R}) , 进而根据 B_{-1}(K,\mathbb{R})=\{0\} , 有 \dim C_k(K,\mathbb{R})=\dim B_{k-1}(K,\mathbb{R})+\dim Z_k(K,\mathbb{R}) , 因此有
\begin{align*} \sum_{k \geq 0}(-1)^kn_k=\sum_{k \geq 0}(-1)^k\dim C_k(K,\mathbb{R})=\sum_{k \geq 0}(-1)^k\dim B_{k-1}(K,\mathbb{R})+\sum_{k \geq 0}(-1)^k\dim Z_k(K,\mathbb{R}) \end{align*}\\ \begin{align*} \sum_{k \geq 0}(-1)^kb_k=\sum_{k \geq 0}(-1)^k\dim H_k(K,\mathbb{R})=\sum_{k \geq 0}(-1)^k\dim Z_k(K,\mathbb{R})-\sum_{k \geq 0}(-1)^k\dim B_k(K,\mathbb{R}) \end{align*}\\
即上面两式的右边相等 , 故有 \displaystyle\sum_{k \geq 0}(-1)^kn_k=\sum_{k \geq 0}(-1)^kb_k , Poincaré 公式得证 .
Poincaré 定理确实可以找到 Gauss-Bonnet 公式和 Riemann-Roch 公式的共同点 ,且 Poincaré 的同调论之后的发展有两个演变 , 分别是同调群的分析化——De Rham 上同调和以层为系数的上同调群——层上同调 .
3.同调群与 de Rham 上同调

同调论是研究空间的重要工具 , 如研究 Euclid 空间就产生了Eucliden Geometry , 研究 Riemann 流形就有了 Riemannian Geometry , 而同调论是研究微分流形而产生的 .
Riemann 提出了比 Reimann 面和 Riemann 流形更基本的概念——微分流形 , 如果在 2 维微分流形上引进复坐标就得到了 Reimann 面 , 在微分流形上确定一个 Riemann 度规后就得到了 Riemann 流形 , 故微分流形有下面的性质 , 即在流形上的每一个点的附近存在局部坐标系 , 且满足不同坐标系之间的坐标变换在公共坐标邻域内是无限次可微的 .
事实上以同调论为核心的代数拓扑学的发展也起源于微分流形的研究 , 首先我们来看一个微分流形的例子 , 即当 x,y,z 是复数时 , 由 f(x,y,z)=0 确定的图形是四维曲面 , 其中 f 是多项式 , Poincaré 曾经用分析的方法研究这个四维微分流形 , 也希望找到研究 n 维微分流形的方法 , Betti 也专门计算了这个四维微分流形的连通阶数 , 故后来 Poincaré 放弃分析方法而采用剖分的手段来计算 Betti 数 , 导致了不再采用坐标来研究微分流形了 , 但我们仍然认为同调论来源于分析 , 最具有代表性的就是法国的大数学家 Cartan , 他在计算紧 Lie 群的同调时没有采用剖分的方法而是根据分析的方法 , 即利用 Lie 群上的微分式和外微分算子来定义 de Rham 上同调群 , 后来由 de Rham 证明了 Cartan 的断言——上同调群的维数就是 Betti 数 , 这就是 de Rham 定理 .
剖分方法和分析方法的差别在于 , 剖分采用积分限来处理同调而分析采用微分式 (即积分中的被积函数) , 虽然两种不同但 Stokes 公式却将积分限和被积函数联系在了一起 .
下面我们来看最简单的一次微分式——一个单变量函数 f(x) 的微分 df , 而 df 是差分 f(x+\Delta x)-f(x) 中的主要线性部分 , 后来就有了导数的定义 , 即函数关于自变量 x 的导数为 \displaystyle\frac{\partial f}{\partial x}=\lim\limits_{\Delta x\rightarrow 0}\frac{f(x+\Delta x)-f(x)}{\Delta x} , 从导数的定义可知 , 导数和自变量的选取有关 , 若取另一个自变量 y , 一般有 \displaystyle\frac{\partial f}{\partial y} \neq \frac{\partial f}{\partial x} , 但两者有如下的关系 \displaystyle\frac{\partial f}{\partial x}=\displaystyle\frac{\partial f}{\partial y}\cdot\displaystyle\frac{\partial y}{\partial x} , 于是就可以给出微分的定义 .
定义(微分)：设 f 是 \mathbb{R} 上的函数 , 映射 F:\mathbb{R}\{x\} \to \mathscr{F}(\mathbb{R}) 由 F(\{x\})=\displaystyle\frac{\partial f}{\partial x} 来定义 , 其中 \{x\} 是 \mathbb{R} 上的任意一个坐标 , \mathbb{R}\{x\} 是 \mathbb{R} 上所有坐标的集合 , \mathscr{F}(\mathbb{R}) 是 \mathbb{R} 上所有可微函数的集合 , 则称 F 为函数 f 的微分且记作 df .
在微分几何中则是将一次微分式定义为一个一次反变张量或向量场集合上的线性函数 , 微分几何中采用这样的定义的动机在于可以推广到高维情形 , 本文我们并不打算用向量场的方式来定义微分 , 事实上向量场和微分式既彼此独立又相互等价 , 接下来从微积分的角度来描述微分式甚至是高次微分式 , 我们来看一个关于 \mathbb{R}^n 或 M^n 中的微分式的定理 .
定理1：设 U 是 \mathbb{R}^n 中的一个开集 , 则有 \Lambda^s(U) 且 s=0,1,…,n , 其中 \Lambda^0(U) 是 U 上的可微函数集合 , 当 s \geq n+1 时 , 规定 \Lambda^s(U)=0 , 于是在这些 \Lambda^s(U) 中有加法 + , 乘法 \wedge 和外微分算子 d , 即
\begin{align*} &+：\Lambda^s(U) \times \Lambda^s(U) \to \Lambda^s(U)~,~(\omega_1,\omega_2) \mapsto \omega_1+\omega_2\\ &\wedge：\Lambda^r(U) \times \Lambda^s(U) \to \Lambda^{r+s}(U)~,~(\omega_1,\omega_2) \mapsto \omega_1 \wedge \omega_2\\ &d：\Lambda^r(U) \to \Lambda^{r+1}(U)~,~\omega \to d\omega  \end{align*}\\
且满足下面的法则：
(i) 关于加法 + , 有结合律和交换律 , 即 (\omega_1+\omega_2)+\omega_3=\omega_1+(\omega_2+\omega_3) 和 \omega_1+\omega_2=\omega_2+\omega_1 ;
(ii) 关于乘法 \wedge , 有结合律和反交换律 , 即 (\omega_1 \wedge \omega_2) \wedge \omega_3=\omega_1 \wedge (\omega_2 \wedge \omega_3) 和 \omega_1 \wedge \omega_2=(-1)^{rs}\omega_2 \wedge \omega_1 , 其中 \omega_1 \in \Lambda^r(U) 和 \omega_2 \in \Lambda^s(U) ;
(iii) 关于外微分算子 d , 有 d^2=0 ;
(iv) 关于 + 和 \wedge , 有 \omega \wedge (\omega_1+\omega_2)=\omega \wedge \omega_1+\omega \wedge \omega_2 ;
(v) 关于 + 和 d , 有 d(\omega_1+\omega_2)=d\omega_1+d\omega_2 ;
(vi) 关于 \wedge 和 d , 有 d(\omega_1 \wedge \omega_2)=d\omega_1 \wedge \omega_2+(-1)^r\omega_1 \wedge d\omega_2 和 d(\omega_1 \wedge \omega_2)=(-1)^sd\omega_1 \wedge \omega_2+\omega_1 \wedge d\omega_2 , 其中 \omega_1 \in \Lambda^r(U) 和 \omega_2 \in \Lambda^s(U) ;
定理1定义了 U 的微分式 , 如果 U_1 和 U_2 是 \mathbb{R}^n 中的两个开集且 U_2 \subset U_1 , 则 U_1 中的函数可以限制在 U_2 上 , 就可以得到类似的微分式的性质 , 即若 \omega \in \Lambda^s(U_1) , 则 \omega 限制在 U_2 上的微分式为 \omega|_{U_2} \in \Lambda^s(U_2) , 因此有下面的定理 .
定理2：设 U_1 和 U_2 是 \mathbb{R}^n 中的两个开集 , 若有 \omega_1 \in \Lambda^s(U_1) 和 \omega_2 \in \Lambda^s(U_2) 且满足 \omega_1|_{U_1 \cap U_2}=\omega_2|_{U_1 \cap U_2} , 则存在唯一的 \omega \in \Lambda^s(U_1 \cup U_2) 使得 \omega|_{U_1}=\omega_1 和 \omega|_{U_2}=\omega_2 ; 反之若 \omega \in \Lambda^s(U_1 \cup U_2) 且 \omega|_{U_i}=\omega_i~(i=1,2) , 则有 \omega_1|_{U_1 \cap U_2}=\omega_2|_{U_1 \cap U_2} .
根据定理2就可以定义 n 维微分流形 M 上的微分式 , 由于微分流形的各个局部都有坐标系 , 故取 M 的坐标邻域的有限覆盖 \{U_i\} , 即 M=\displaystyle\bigcup_{i=1}^NU_i , 则对于 \omega_i \in \Lambda^s(U_i) , 其中 i=1,2,…,N , 且满足 \omega_i|_{U_i \cap U_j}=\omega_i|_{U_i \cap U_j}~,~\,\forall\,i,j 时 , 故称 \{\omega_1,\omega_2,…,\omega_N\} 是 M 上的一个 s 次微分式 \omega , 进而有 \omega|_{U_i}=\omega_i , 而所有的 \omega 构成的集合就是 \Lambda^s(M) , 此时定理1仍然成立 .
下面我们再来看两个定理 , 这两个定理也给出了微分式的性质 .
定理3：设 M,N 分别为 m,n 维流形 , 且 f:M \to N 是可微映射 , 则存在一个映射 f^*: \Lambda^k(N) \to \Lambda^k(M) 使得
f^* \left( \displaystyle\sum_{i_1,i_2,…,i_k} dx_{i_1} \wedge dx_{i_2} …\wedge dx_{i_k}  \right)=\sum_{i_1,i_2,…,i_k}^n\sum_{\alpha_1,\alpha_2,…,\alpha_k}^m(g_{i_1,i_2,…,i_k} \circ f)\frac{\partial x_{i_1}}{\partial y_{\alpha_1}}\frac{\partial x_{i_2}}{\partial y_{\alpha_2}}…\frac{\partial x_{i_k}}{\partial y_{\alpha_k}}dy_{\alpha_1} \wedge dy_{\alpha_2} \wedge … \wedge dy_{\alpha_k} \\
其中 (y_1,y_2,…,y_m) 和 (x_1,x_2,…,x_n) 分别是流形 M 和 N 的局部坐标系 , 故 f^* 有加法 + , 乘法 \wedge 和外微分算子 d , 即满足 f^*(\omega_1+\omega_2)=f^*(\omega_1)+f^*(\omega_2) , f^*(\omega_1 \wedge \omega_2)=f^*(\omega_1) \wedge f^*(\omega_2) 和 d(f^*(\omega))=f^*(d(\omega)) .
定理4：设 f 是 M 上的函数 , 则有 df=\displaystyle\sum_{i}\frac{\partial f}{\partial x_i}dx_i .
因此对于微分流形 M ,  (\Lambda^k(M),+,\wedge,d,f^*) 及其性质构成了微分流形上的一个系统 , 这为从微分式的系统中导出同调群奠定了基础 , 称为 de Rham 上同调 . 由定理1得到 de Rham 复形列为 0 \rightarrow \Lambda^0(M) \xrightarrow{d} \Lambda^1(M) \xrightarrow{d}… \xrightarrow{d} \Lambda^n(M) \rightarrow 0 且满足 d^2=0 , 以及边缘算子 \partial:C_k(K,\mathbb{R}) \to C_{k-1}(K,\mathbb{R}) , 其中 C_k(K,\mathbb{R}) 是 k 维链群且满足 \partial^2=0 , 故单纯复形的剖分 K 的下链复形列 0 \rightarrow C_n(K,\mathbb{R}) \xrightarrow{\partial} C_{n-1}(K,\mathbb{R}) \xrightarrow{\partial} … \xrightarrow{\partial} C_0(K,\mathbb{R}) \rightarrow 0 , 由于 k 维同调群为  H_k(K,\mathbb{R})=\displaystyle\frac{Z_k(K,\mathbb{R})}{B_k(K,\mathbb{R})} , 其中 Z_k(K,\mathbb{R})=Ker\{\partial:C_k(K,\mathbb{R}) \to C_{k-1}(K,\mathbb{R})\}=\{\alpha \in C_k(K,\mathbb{R})~|~\partial\alpha=0\} 和 B_k(K,\mathbb{R})=Im\{\partial:C_k(K,\mathbb{R}) \to C_{k-1}(K,\mathbb{R})\}=\partial C_{k+1}(K,\mathbb{R}) , 因此从 de Rham 复形可以定义 k 维 de Rham 上闭链群 Z_{dR}^k(M)=Ker\{d:\Lambda^k(M) \to \Lambda^{k+1}(M)\} , k 维 de Rham 上边缘链群 B_{dR}^k(M)=Im\{d:\Lambda^{k-1}(M) \to \Lambda^k(M)\} 和 k 维 de Rham 上同调群 H_{dR}^k(K,\mathbb{R})=\displaystyle\frac{Z_{dR}^k(K,\mathbb{R})}{B_{dR}^k(K,\mathbb{R})} , 事实上 C_k(K,\mathbb{R}) , Z_k(K,\mathbb{R}) , B_k(K,\mathbb{R}) 和 H_k(K,\mathbb{R}) 都是有限维实向量空间 , 而 \Lambda^k(M) , Z_{dR}^k(K,\mathbb{R}) 和 B_{dR}^k(K,\mathbb{R}) 是无穷维的 , 然后 H_{dR}^k(K,\mathbb{R}) 是有限维的且维数等于 M 的第 k 个 Betti 数 b_k , 这一结论可以下面的 de Rham 定理给出 .
定理(de Rham)：设 M 是一个 n 维微分流形 , K 是 M 的一个单纯复形的剖分 , 则存在一个线性空间的同构 \Phi_*:H_{dR}^k(K,\mathbb{R}) \to Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R})~,~\,\forall\,k=0,1,…,n , 其中 Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R})=\{f:H_k(K,\mathbb{R}) \to \mathbb{R}~|~f 是实线性映射\} .
由 de Rham 定理可知 , 与 H_{dR}^k(K,\mathbb{R}) 更接近的不是 H_k(K,\mathbb{R}) 而是 Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R}) , 这一点也可以从 H_k(K,\mathbb{R}) 和 H_{dR}^k(K,\mathbb{R}) 的定义得到 , 即两者有区别 , 接下来对比下面两个复合形 0 \rightarrow C_n(K,\mathbb{R}) \xrightarrow{\partial} C_{n-1}(K,\mathbb{R}) \xrightarrow{\partial} … \xrightarrow{\partial} C_0(K,\mathbb{R}) \rightarrow 0 和 0 \rightarrow \Lambda^0(M) \xrightarrow{d} \Lambda^1(M) \xrightarrow{d}… \xrightarrow{d} \Lambda^n(M) \rightarrow 0 , 故两个复形列的方向相反 , 称前者为下复形列 , 后者为上复形列 , 进而分别得到的同调群为下同调群和上同调群 . 然后构造一个复形列 0 \rightarrow C^0(K,\mathbb{R}) \xrightarrow{\delta} C^1(K,\mathbb{R}) \xrightarrow{\delta} … \xrightarrow{\delta} C^n(K,\mathbb{R}) \rightarrow 0 , 使得它的上同调群 H^k(K,\mathbb{R}) 同构于 Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R}) , 此时将 de Rham 同构表示为 \Psi:H_{dR}^k(K,\mathbb{R}) \simeq H^k(K,\mathbb{R}) , 因此上面的复形列定义如下 , 令 C^k(K,\mathbb{R})=Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R}) , 且 \delta:C^k(K,\mathbb{R}) \to C^{k+1}(K,\mathbb{R})~,~a \mapsto \delta a 满足 (\delta a)\alpha=a(\partial \alpha)~,~\,\forall\,\alpha \in C_{k+1}(K,\mathbb{R}) , 其中 a 是 0-单形(顶点) .
现在我们来讨论 H^k(K,\mathbb{R}) 与 Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R}) 之间是同构的 . 由于线性空间的同态 \alpha:Hom_{\mathbb{R}}(C_k(K,\mathbb{R}),\mathbb{R}) \to Hom_{\mathbb{R}}(Z_k(K,\mathbb{R}),\mathbb{R}) 和 \beta:Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R}) \to Hom_{\mathbb{R}}(Z_k(K,\mathbb{R}),\mathbb{R}) 分别由映射 \alpha':Z^k(K,\mathbb{R}) \to C^k(K,\mathbb{R}) 和 \beta':Z^k(K,\mathbb{R}) \to H^k(K,\mathbb{R})=\displaystyle\frac{Z^k(K,\mathbb{R})}{B^k(K,\mathbb{R})} 诱导出来 , 其中 \alpha' 是嵌入映射以及 \beta' 是自然投射 , 故有
(i) 存在唯一同态 \eta:Z^k(K,\mathbb{R}) \to Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R}) 使得下面的交换图成立 , 即
\begin{align*} \quad \begin{CD}   Z^k(K,\mathbb{R}) @>^{}>> Hom_{\mathbb{R}}(C_k(K,\mathbb{R}),\mathbb{R})\\  @V^{\displaystyle\eta}VV@V^{\displaystyle\alpha}VV\\  Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R}) @>^{\displaystyle\beta}>> Hom_{\mathbb{R}}(Z_k(K,\mathbb{R}),\mathbb{R})  \end{CD} \end{align*}\\
(ii) B^k(K,\mathbb{R}) \subset Ker(\eta)=\eta^{-1}(0) , 进而得到 \eta_*:Z^k(K,\mathbb{R}) \to Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R}) 是同构 .
再根据 de Rham 定理可知 , \Phi_*:H_{dR}^k(K,\mathbb{R}) \to Hom_{\mathbb{R}}(H_k(K,\mathbb{R}),\mathbb{R}) 和 \Psi=\eta_*^{-1}\Phi_*:H_{dR}^k(K,\mathbb{R}) \to H^k(K,\mathbb{R}) 都是自然同构 .
最后我们再来讨论一下同构 \Phi_* 或 \Psi 的定义 . 设 \omega \in \Lambda_k(M) , 对于单纯复形的剖分 K 中的每一个 k 维定向单形 \overrightarrow{\sigma} 且在 \overrightarrow{\sigma} 上任取坐标系 \{u_1,u_2,…,u_k\} , 此时 \omega 限制在 \sigma 上就表示为 \omega|_{\sigma}=g(u_1,u_2,…,u_k)du_1 \wedge du_2 \wedge … \wedge du_k , 其中 \sigma 是 \overrightarrow{\sigma} 去掉定向后的几何单形 , 故可以得到下面的定理 .
定理5：给定 \omega \in \Lambda^k(M) 和 \overrightarrow{\sigma} , 则 \varepsilon(\overrightarrow{\sigma} , \{u_1,u_2,…,u_k\}) 和 \displaystyle\int_{\sigma}g(u_1,u_2,…,u_k)du_1 \wedge du_2 \wedge … \wedge du_k 的乘积是一个与坐标系 \{u_1,u_2,…,u_k\} 无关的数 , 即 \displaystyle\int_{\overrightarrow{\sigma}}\omega=\varepsilon(\overrightarrow{\sigma} , {u_1,u_2,…,u_k})\int_{\sigma}g(u_1,u_2,…,u_k)du_1 \wedge du_2 \wedge … \wedge du_k\\ 其中 \varepsilon(\overrightarrow{\sigma} , \{u_1,u_2,…,u_k\}) 的取值依赖于 \sigma 的定向和坐标系 \{u_1,u_2,…,u_k\} 的定向 , 即只可能取 \pm 1 .
根据定理5可以得到定理6中的两条性质 .
定理6：(i) \displaystyle\int_{\overrightarrow{\sigma}}\omega=-\int_{\overleftarrow{\sigma}}\omega ; (ii) \displaystyle\int_{\overrightarrow{\sigma}}d\omega=\int_{\partial \overrightarrow{\sigma}}\omega .
定理6中的性质(i)是 trivial 的 , 而性质(ii)是 Stokes 公式 . 而利用定理5和定理6可以定义映射 \theta:\Lambda^k(M) \to Hom_{\mathbb{R}}(C_k(K,\mathbb{R}),\mathbb{R})=C^k(K,\mathbb{R}) 满足对任意的 \omega \in \Lambda^k(M) 和 \displaystyle\sum_{i=1}^lc_i\overrightarrow{\sigma_i} \in C_k(K,\mathbb{R}) , 有 \theta(\omega)(\displaystyle\sum_{i=1}^lc_i\overrightarrow{\sigma_i})=\sum_{i=1}^lc_i\int_{\overrightarrow{\sigma_i}}\omega , 其中 \displaystyle\sum_{i=1}^lc_i\overrightarrow{\sigma_i} 是单纯复形的剖分 K 中 k 维单形的线性组合(即 k 维链) , 且由定理6的性质(ii)可知 , 有 \theta d=\delta\theta , 进而得到 \theta(Z_{dR}^k(K,\mathbb{R})) \subset Z^k(K,\mathbb{R}) 和 \theta(B_{dR}^k(K,\mathbb{R})) \subset B^k(K,\mathbb{R}) , 因此由 \theta 诱导出映射 \theta_*:H_{dR}^k(K,\mathbb{R}) \to H^k(K,\mathbb{R}) , 此时 \theta_*=\Psi , 这就说明了 \Phi_* 或 \Psi 是同构 , 它将流形上的微积分和空间剖分的代数方法联系在了一起 .
4.层与上同调

我们已知同调论的一大作用是将 Gauss-Bonnet 公式和 Riemann-Roch 公式联系起来 , 事实上 Gauss-Bonnet 公式中的 Euler 数的那一项用同调的观点看就是 betti 数或同调群维数的交错和 , 那么如果对 Riemann-Roch 公式中某些项用同调论的方法来处理 , 即解释为某种同调群的维数的较粗和 , 就可以进一步把 Riemann-Roch 定理推广到高维情形 , 这个问题直到20世纪50年代由数学家 Kodaira.K. 和 Serre.J.P. 解决 , 同时 Hirzebruch.F. 提出并证明了高维情形下的 Riemann-Roch 公式 , 因此就得到了 Hirzebruch-Reimann-Roch 定理 , 而 Kodaira 和 Serre 解决这一问题时用的同调论是以层为系数的上同调群——层上同调 .
上一节中我们提到的 de Rham 定理起初是在1928年由 de Rham 完成最原始的证明 , 后来 weil 给出了新的证明 , 对层论的发展起了决定性的作用 , 再由 H.Cartan 进一步发展就得到了现代层论 , 包括层的定义 , 以层为系数的上同调群及其应用等 .
由于 de Rham 同构可以表示为 \Psi:H_{dR}^k(K,\mathbb{R}) \to H^k(K,\mathbb{R}) , 这个同构是根据微分式的积分诱导出来的 , 如果用现代层论的观点来看 weil 的证明 , 则我们可以了解到他构造了一系列的群 A^{0,k},A^{1,k-1},…,A^{k,0},B^{k,0},B^{k-1,1},…,B^{0,k} 和一个交换图 , 即


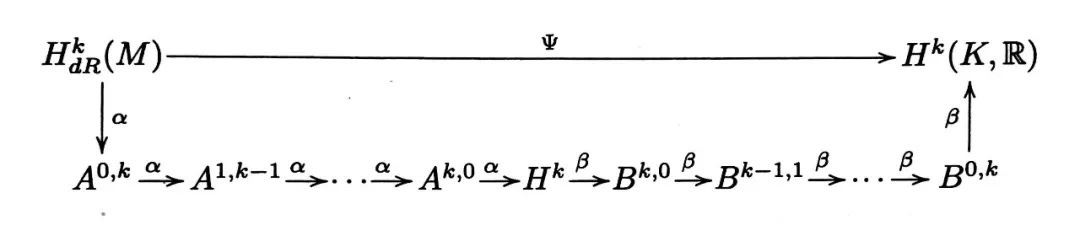
使得 \alpha 和 \beta 均为同构 , 进而得到 \Psi 是同构 , 这就证明了 de Rham 定理 , 其中 A^{*,*} , B^{*,*} 和 H^k 都是 n 维微分流形 M 上某类层的上同调群 .
接下来我们开始讨论层与层的上同调群 , 本文引入层的目的是为了将 Gauss-Bonnet 公式和 Riemann-Roch 定理统一起来 , 事实上在流形上的分析主要分为两个方面 , 其一是研究局部性质 , 另外一个是研究整体性质 , 而层论的作用就是在两者之间建立联系 , 故设 M 是一个微分流形 , 取 M 上的一个有限开覆盖 \mathscr{U}=\{U_i~|~i=1,2,…,N\} , 假设要讨论某一几何量 , 那么既可以在整个流形 M 上讨论其整体性质 , 也可以在各个 U_i 上讨论其局部性质 , 故层论将在 U_i 上得到的结果通过良好的粘合传递到 M 上 , 如果想要研究 M 上的 k 次微分式空间 \Lambda^k(M) 的性质 , 则先考虑集合 \{\Lambda^k(U_i)~|~i=1,2,…,N\} 中每一个 \Lambda^k(U_i) , 此时这个集合就是 M 上的一个层 , 这正好符合从局部到整体的研究方法 .
定义(层)：设 M 是 n 维微分流形 , \mathscr{U}=\{U_i~|~i=1,2,…,N\} 是 M 的一个有限开覆盖 , 再令 \mathscr{B}(\mathscr{U}) 是 M 中的一些开集构成的集合 , 而这些开集都是 \mathscr{U} 中的元素经过有限次交或并运算得到 , 对于每个 U \in \mathscr{B}(\mathscr{U}) 对应一个交换群 \mathscr{F}(U) , 以及对于任意的 U,V \in \mathscr{B}(\mathscr{U}) 且满足 V \subset U , 则存在一个群同态 \rho_{UV}:\mathscr{F}(U) \to \mathscr{F}(V) 使得下面的结论成立
(i) 对于任意的 U,V,W \in \mathscr{B}(\mathscr{U}) , 若 W \subset V \subset U , 则有 \rho_{UW}=\rho_{VW} \circ \rho_{UV} ;
(ii) 若 V_1,V_2,…,V_{\alpha} \in \mathscr{B}(\mathscr{U}) 和 V=\displaystyle\bigcup_{i=1}^{\alpha}V_i , 以及如果 f,g \in \mathscr{F}(V) 满足 \rho_{VV_i}(f)=\rho_{VV_i}(g)~,~\,\forall\,i=1,2,…,\alpha , 则有 f=g ;
(iii) 若 V_1,V_2,…,V_{\alpha} \in \mathscr{B}(\mathscr{U}) 和 V=\displaystyle\bigcup_{i=1}^{\alpha}V_i , 且 f_i \in \mathscr{F}(V_i)~,~\,\forall\,i=1,2,…,\alpha 满足 \rho_{V_i,V_i \cap V_j}(f_i)=\rho_{V_j,V_i \cap V_j}(f_j)~,~\,\forall\,i,j=1,2,…,\alpha , 则存在 f \in  \mathscr{F}(V) 使得 \rho_{VV_i}(f)=f_i~,\,\forall\,i=1,2,…,\alpha ;
因此称 \{\mathscr{F}(V),\rho_{UV}\} 为 M 上的一个层(sheaf) .
根据层的定义可知 , 令 \mathscr{F}(U)=\Lambda^k(U) 且 \rho_{UV}: \Lambda^k(U) \to \Lambda^k(V) 为限制映射 , 则 \{\Lambda^k(U),\rho_{UV}\}_\mathscr{U} 是一个层 ; 又设 M 是 Reimann 面且 \mathscr{U} 是 M 的一个有限开覆盖 , 对于任意的 U \in \mathscr{B}(\mathscr{U}) , 以及 \mathscr{O}(U) 是 U 上全纯函数的集合且在加法法则下构成群 , 则对于 V \subset U \in \mathscr{B}(\mathscr{U}) , 故 \rho_{UV}:\mathscr{O}(U) \to \mathscr{O}(V) 为限制映射 , 则 \{\mathscr{O}(U),\rho_{UV}\}_\mathscr{U} 是一个层 .
设 \mathscr{U} 是 n 维微分流形的一个有限开覆盖 , 而 \{\mathscr{F}(V),\rho_{UV}\} 是 M 上的一个层 , 故有下面的定义：
(i) 一个以 \mathscr{F} 为系数的 q 维上链 f 定义为对 \mathscr{U} 中的任意 q+1 个开集 W_0,W_1,…,W_q , 有
f(W_0,W_1,…,W_q)=\begin{cases} 0~,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~W_0,W_1,…,W_q=\varnothing\\ \mathscr{F}(W_0 \cap W_1 \cap … \cap W_q)~,~W_0,W_1,…,W_q \neq\varnothing \end{cases} \\
于是所有以 \mathscr{F} 为系数的 q 维上链的集合记作 C^q(\mathscr{U},\mathscr{F}) .
(ii) 上边缘算子 \delta:C^q(\mathscr{U},\mathscr{F}) \to C^{q+1}(\mathscr{U},\mathscr{F}) 由 (\delta f)(W_0,W_1,…,W_{q+1})=\sum_{i=0}^{q+1}(-1)^i\rho_{U_iV}f(W_0,W_1,…,\widehat{W_i},…W_{q+1})\\ 来定义 , 其中 U_i=W_0 \cap W_1 \cap … \cap \widehat{W_i} \cap … \cap W_{q+1} , 而 \widehat{W_i} 表示在 U=W_0 \cap W_1 \cap … \cap W_{q+1} 中不出现第 i 个开集 W_i . 事实上有 \delta \circ \delta=0 .
(iii) q 维上闭链群和 q 维上边缘链群分别定义为 Z^q(\mathscr{U},\mathscr{F})=\{f \in C^q(\mathscr{U},\mathscr{F})~|~\delta f=0\} 和 B^q(\mathscr{U},\mathscr{F})=\delta C^{q-1}(\mathscr{U},\mathscr{F}) .
(iv) 定义以 \mathscr{F} 为系数的 q 维上同调群为 H^q(\mathscr{U},\mathscr{F})=\displaystyle\frac{Z^q(\mathscr{U},\mathscr{F})}{B^q(\mathscr{U},\mathscr{F})} .
上面定义的 H^q(\mathscr{U},\mathscr{F}) 与 \mathscr{U} 的取法有关 , 这在 \mathscr{F} 的定义和同调群的构造中得以体现 , 此时可以将 \mathscr{F} 改成 \mathscr{F}_{\mathscr{U}} , 然后就可以提出一个问题——在自然同构意义下各个 H^q(\mathscr{U},\mathscr{F}_{\mathscr{U}}) 是否彼此同构？事实上如果覆盖 \mathscr{U} 越细密 , 则 H^q(\mathscr{U},\mathscr{F}_{\mathscr{U}}) 会越来越趋近于某个同调群 \widehat{\mathscr{F}} , 进而得到如果用 \mathscr{U} \to 0 表示覆盖 \mathscr{U} 越来越细地趋于极限状态且同调群极限也存在 , 则下列的关于极限的等式 \lim\limits_{\mathscr{U} \rightarrow 0}H^q(\mathscr{U},\mathscr{F}_{\mathscr{U}})=\lim\limits_{\mathscr{U} \rightarrow 0}H^q(\mathscr{U},\lim\limits_{\mathscr{U} \rightarrow 0}\mathscr{F}_{\mathscr{U}}) 成立 , 令 \widehat{\mathscr{F}}=\lim\limits_{\mathscr{U} \rightarrow 0}\mathscr{F}_{\mathscr{U}} , 于是有 H^q(M,\widehat{\mathscr{F}})=\lim\limits_{\mathscr{U} \rightarrow 0}H^q(\mathscr{U},\widehat{\mathscr{F}}) , 下面我们只需证明 H^q(M,\widehat{\mathscr{F}})=H^q(\mathscr{U},\mathscr{F}) 就可以解决各个 H^q(\mathscr{U},\mathscr{F}_{\mathscr{U}}) 的同构问题 .
因此可以从两个方法来处理 \widehat{\mathscr{F}} , 第一种办法是用最初始的层的定义 , 即存在映射 \pi:\widehat{\mathscr{F}} \to M , 且当 x \in M 时 , 将 \widehat{\mathscr{F}}_x=\pi^{-1}(x) 表示为 \lim\limits_{\mathscr{U} \rightarrow 0}\{\mathscr{F} 在点 x 处的函数芽的集合\} , 第二种方法是在本文的层的定义中把 \mathscr{U} 取作 M 的所有开集构成的集合 , 此时存在一个不依赖于覆盖 \mathscr{U} 的最大层 \widehat{\mathscr{F}} , 尽管两种方法定义的 \widehat{\mathscr{F}} 不同 , 但最后得到的同调群 H^q(M,\widehat{\mathscr{F}}) 却是一样的 , 后来 Čech 给出了 H^q(M,\widehat{\mathscr{F}}) 的定义 , 称为 Čech 上同调 , 事实上有个 Leray 定理将 H^q(M,\widehat{\mathscr{F}}) 和 H^q(\mathscr{U},\mathscr{F}) 放在一起 , 定理内容表述为如果开覆盖 \mathscr{U} 取得足够良好 , 则有 H^q(M,\widehat{\mathscr{F}})=H^q(\mathscr{U},\mathscr{F}) , 因此我们可以看到层上同调就是一种强有力的工具(刚性) , 在下一篇文章讨论高维情形下的 Riemann-Roch 定理时将发挥 H^q(M,\widehat{\mathscr{F}}) 和 H^q(\mathscr{U},\mathscr{F}) 各自的优势 .

胡来财

写得太好了[赞][赞][赞]

感悟顿觉

话说这么好的文章为啥没啥人看啊，科普科普不是挺好[大笑][赞][赞]

就是喜欢怼

抄的书，然后顺便加入一小点自己的想法

三千疯人院

感谢