|
|
将一枚硬币抛到地面上,结果要么正面朝上要么反面朝上。假如今天你从你的无尽的硬币库存中取出了 N 个硬币,并在无尽的地面上依次投掷取出的每一枚硬币,投掷好的硬币你会将他们按照投掷顺序依次排成一排。如果存在连续排列的三个硬币都是正面或者都是反面,那么这个排列是丑陋的,反之这个排列就是美观的。问:这 N 个硬币来排列,有多少个丑陋的排列? Standard Input
一个正整数 N (1 \leq N \leq 10000),表示硬币的个数。
Standard Output
输出一个整数,即丑陋排列的个数。
Samples
source: Lutece (uestc.edu.cn) 一、题目来源
题目是学校一门选修课的算法实践题目,给到题目的标签是【动态规划】。由于花了不少时间去思考,觉得这题很有意思,所以有了这篇记录(可能因为我不是ACMer所以觉得,对我还是挺有难度的/(ㄒoㄒ)/~~)
二、简单分析
以Sample为例,N=4,我们假设'1'代表正面朝上,'0'代表反面朝上,那么满足题目的“丑陋的”排列有:1110,0111,1111,0001,1000,0000. 可以发现,N=4时,在正反两种情况中有“对称”的形式,并且可以只考虑【连续排列的三个硬币都是正面】,再对结果乘2即可,那么这种规律对一般的N成立么?
三、简化问题
我们先考虑一个简化版的问题:连续抛N次硬币,至少连续两次都是正面朝上的情况数。
再简化一下,我们先考虑N=10的情况。并且我们定义一个数列 A_n^k :表示抛掷n次硬币,连续k次正面朝上的情况数。显然这里我们将先考虑 A_{10}^2
连续抛10次硬币,那么第一次抛出后要么正面朝上,要么反面朝上(以*表示任意情况):
1*********(情况1)
0*********(情况2)
11********(情况1.1)
10********(情况1.2)
对于情况1.1,这显然已经满足了【至少连续两次都是正面朝上】的要求,剩下的8次还不是爱 咋咋地?也就是 2^8 种。
对于情况1.2,抛出了反面,而我们要求连续的正面朝上,所以又被回原形了(重新开始),也就是 A_{8}^2 种。
- 对于情况2:抛出反面直接重新开始, A_{9}^2 种。
于是我们得到了递推式: A_{10}^2 = 2^8+A_{8}^2+A_{9}^2
根据以上思路,我们容易得到一般情况的递推式(状态转移方程): A_{n}^k = 2^{n-k}+ \sum_{i=1}^{k}A_{n-i}^k
至此,这个简化版的问题我们已经顺利解决了,那么能否直接根据这个递推式得到原问题的状态转移方程呢?或许又,但本菜鸡还没有搞出来,直接乘2肯定是行不通的,会有重复的计算,欢迎交流讨论。But,这个思路是一个非常好的思路,根据这个思路,我最种得到了原问题的状态转移方程。
四、解决原问题
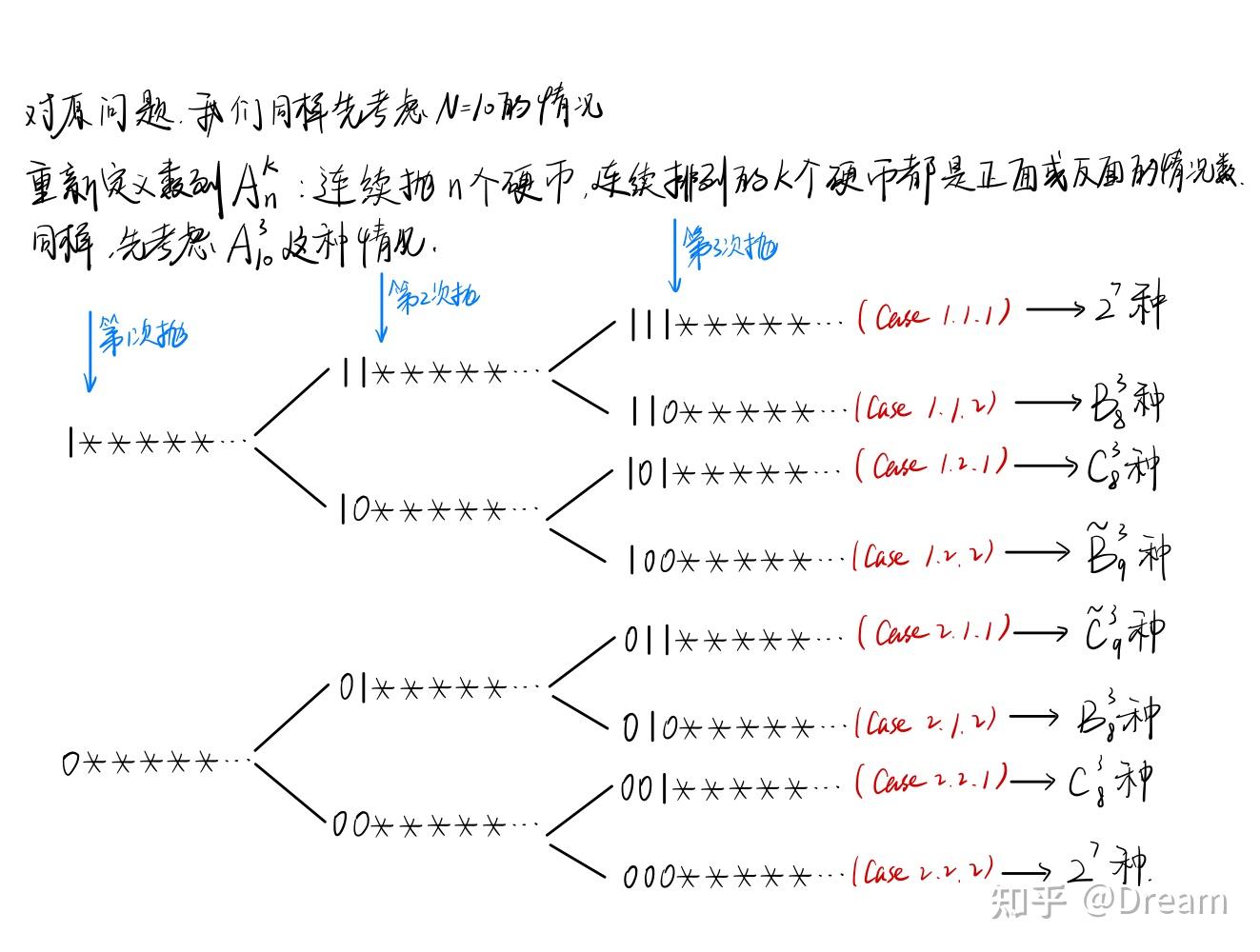
大部分的思路都体现在以上的推导了。上面的推到中出现了 B_{n}^k 、 \widetilde{B}_{n}^k 、 C_{n}^k 、 \widetilde{C}_{n}^k 这四个新的数列,这是在推导过程中发现这6种情况并不能简单的根据 A_{n}^k 来递推地表示(不知这在动态规划中是否有其专门的名字,非ACMer表示不是很了解,也还没有刷过力扣/(ㄒ_ㄒ)/).
B_{n}^k :表示连续抛n个硬币(其中第一次确定是反面朝上),连续排列的三个硬币都是正面或都是反面。
\widetilde{B}_{n}^k :表示连续抛n个硬币(其中第一、二次确定是反面朝上),连续排列的三个硬币都是正面或都是反面。
C_{n}^k :表示连续抛n个硬币(其中第一次确定是正面朝上),连续排列的三个硬币都是正面或都是反面。
\widetilde{C}_{n}^k :表示连续抛n个硬币(其中第一、二次确定是正面朝上),连续排列的三个硬币都是正面或都是反面。
OK,根据以上分析我们得到了递推式: A_{10}^3=2*2^7+2B_{8}^3+2C_{8}^3+\widetilde{B}_{9}^3+\widetilde{C}_{9}^3
对于本题,我们可以容易地得到推广: A_{n}^3=2*2^{n-3}+2B_{n-2}^3+2C_{n-2}^3+\widetilde{B}_{n-1}^3+\widetilde{C}_{n-1}^3
其它的变体读者可自行推导or推广之。
最后,事实上 ,有了以上推广,本题基本上已经解决了,至于B_{n}^k 、 \widetilde{B}_{n}^k 、 C_{n}^k 、 \widetilde{C}_{n}^k各自的递推式,根据以上方法,应该比较容易就能写出来了,最终有这四个递推式即可得到答案。帖一下用python的实现的最终代码吧(程序逻辑非常简单,思考量全在这几个状态转移方程上,程序中以BB代替 \widetilde{B} )
n = int(input())
B,BB,C,CC = [0]*(n+5),[0]*(n+5),[0]*(n+5),[0]*(n+5)
B[3] = BB[3] = C[3] = CC[3] = 1
#动态规划
for i in range(4,n+1):
B = CC[i-1]+B[i-2]+C[i-2]+2**(i-3)
C = BB[i-1]+B[i-2]+C[i-2]+2**(i-3)
BB = C[i-2]+2**(i-3)
CC = B[i-2]+2**(i-3)
answer = 2**(n-3)+2**(n-3)+2*B[n-2]+2*C[n-2]+BB[n-1]+CC[n-1]
if n<3:
print(0)
else:
print(answer)参考文献
抛硬币1000次,至少连续10次正面朝上的概率 详细解答
<hr/>补充:
F(n)=2F(n-1)+(2^{n-3}-A_{n-3}) 来自同学的解答/(ㄒ_ㄒ)/~~,上面的解答虽然看上去繁琐,不过思想还是比较有用吧,欢迎交流讨论,若有错误还请指正! |
|